Introducción
Trataré de compartir un pensamiento que tengo en cuanto a la sustentación de un objeto
móvil en un medio fluido, ya sea este líquido o gaseoso (v.g.: aire). No es que se
quiera rebatir ninguna teoría existente, sino que como apoyatura a éstas, podría
enfocarse desde este otro punto de vista; se llegará, por ambas, a iguales conclusiones.
La conjetura radica en el hecho de que el objeto móvil al desplazarse obtiene de
medio de flotabilidad una densidad efectiva que aumenta con la velocidad; esto es decir,
que a medida que viaja, va barriendo distintos volúmentes del medio aumentando para él
su densidad y por lo tanto su flotabilidad.
Se es consciente de la Ecuación de Cayley de 1779 y todo lo que ello implica, como
puede ver en este enlace. Se
posee conocimiento del principio de funcionamiento del dron, del autogiro, girocóptero,
helicóptero y el avión. Qué son y qué papeles juegan el "ángulo de ataque",
"águlo de flecha" y "ángulo de paso" también son temas que conozco
y no niegan este estudio.
La idea aquí es pensar conceptualmente que un área específica de las alas de un
avión, expuesta a un viento determinado, genera una fuerza de sustentación efectiva.
Esta fuerza sería igualmente determinada si consideramos que existe un "área
efectiva" en las hélices rotativas, estrechamente relacionada con la velocidad del
rotor multiplicada por las áreas de las palas. Esto resultaría en un "área
efectiva" similar a la del avión, generando una fuerza de sustentación equivalente.
Fundamententación teórica
|
Sabemos por
Arquímedes que un objeto se hunde en el agua hasta que desplaza una cantidad de agua
igual a su peso total. En ese punto la fuerza de flotación ascendente es exactamente
igual al peso total del objeto flotante.
|
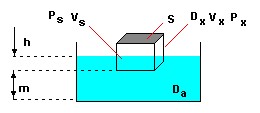
La figura muestra a un objeto de volúmen Vx,
densidad Dx y peso Px flotando con una superficie s en un medio
líquido (por ejemplo agua) de densidad Da. La profundidad de flotación que
denominamos h determinará un volúmen sumergido Vs y un peso del agua que
ocupa Vs. Para simplificar los cálculos pensaremos que la altura m del
recipiente es muchísimo mayor que la flotabilidad h (h << m). Aquí entonces las
ecuaciones de comportamiento serían:
Da = 1 > Dx = Px / Vx
Daef = s . m = Da
Vs = s.h
Px = Psa = Da . Vs = Da . s.h
Þ h = Px
/ s . Da = hreposo
donde Daef es la densidad efectiva del agua. |
|
|
|
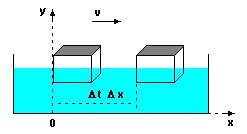
Seguidamente le damos movimiento al objeto a
una velocidad v.
Se proponen las ecuaciones límites:
lim]v=0 Daef = Da
lim]v=¥ Daef
= ¥
; h = 0 ; s = ¥Y pensamos que el área efectiva recorrida
sef aumentará linealmente con la velocidad (aquí k es una constante de
unidades):
sef = (1 + k.v ) s ; k.v > 1
Daef = (1 + k.v ) Da (ecuación que verifica ambas
postulaciones precedentes)
Vs = s.h
Px = Psa = Daef . Vs = Daef . s.h
Þ h = Px
/ s . Daef = Px / s . (1 + k.v ) Da = (Px / s
. Da) / (1 + k.v ) = hreposo / (1 + k.v )
donde se observa que a medida que se desplaza el objeto irá aumentando la
flotabilidad (disminuyendo h).
|
|
|
Ejemplos verificadores de la teoría
Se ha pensado en una serie de casos que podrían explicarse, aparte del enfoque clásico y
ortodoxo de la Física, de igual manera con este enfoque.
Cabe destacar que siempre que un objeto toma flotabilidad (o vuelo si el fluído es
el aire) se deben dar necesariamente dos efectos: la flotabilidad
propiamente dicha y la estabilidad (manutención de su forma sin
inclinarse).
Tenemos los siguientes ejemplos:
Efecto "cabrillas"
O también llamado coloquialmente "efecto cucharita", consiste
en el hecho del planeo que hace en su recorrido una piedra plana lanzada adecuadamente
sobre el agua una y otra vez. Aquí la flotabilidad la hace la velocidad y su estabilidad
la da el giro en símisma.
Elevación del frisbee
Para que se eleve el disco será necesario darle una impulsión de giro. En este
caso la flotabilidad la da el giro y la velocidad su estabilidad.
Elevación de una lancha a motor
Si bien el viento de proa que se recibe lógicamente impulsará a una elevación
del vehículo, entiendo que a esto se le suma el efecto considerado. Si pudiera
experimentarse en una travesía en medio sin atmósfera entiendo que el efecto sería, por
tanto, igualmente notorio aunque con menos intensidad.
Cómodamente podría experimentarse el fecto que presentamos si la nave es una
simple madera fina o tronco longitudinal que termine en punta, tal cual la analogía de un
lápiz, e impulsada por una cuerda.
Independencia de un satélite
Sabemos que podemos hallar la zona geoestacionaria para ubicar un satélite
artificial si igualamos la fuerga gravitatoria terrestre a la fuerza centrífuga. Pero,
aun en esta zona como también en la más alejada, refiriéndome al cosmos propiamente
dicho, aquí no hay materia para la flotabilidad y por tanto tampoco vuelo ordinario.
Explicación del vuelo ecuatorial
Cuando un avión vuela en la línea ecuatorial, no se le suma ni se le resta a su
trayectoria la velocidad de rotación del planeta. Esto es lógico porque está sumergido
en la materia de flotabilidad que es la atmósfera. No es lo mismo si se aleja deella, es
decir, en el cosmos; aquí sí afecta la velocidad de rotación terrestre.
El helicóptero
Las aspas principales impulsan aire hacia abajo aumentando la densidad efectiva de
sustentación, y las posteriores le otorga la estabilidad.
El avión
Las alas principales cumplen la función de otorgar una superficie amplia que,
junto a una velocidad crítica mínima, producirán una densidad efectiva del aire en el
inferior produciendo la flotabilidad, y sus alas pequeñas posteriores si bien ayudarán a
esto están destinadas a mantener la estabilidad. Se verá claramente con el modelo que
describo, que si la altura de vuelo es poca no habrá suficiente densidad efectiva de
sustentación y el avión caerá.
El efecto giroscópico
En este caso no estoy muy seguro, me disculparán por favor si es un disparate,
pero pienso que un disco al girar y cualquiera sea su posición en el espacio, mantendrá
su posición original de giro porque al aumentar las densiades efectivas del aire a sus
ambos lados, ambas atmósferas ejercerán iguales presiones sobre éste mantenindo su
postura. Los siguientes videos serían ejemplificadores: trompo, giróscopo 1 y giróscopo 2; y también habría otro que tal vez pueda también ser entendido
con estos principios (el peso medio total que acusa la balanza no cambia al girar y es la
suma de la del sujeto más la del artefacto).
Puede verificar esto en los Apéndices más abajo con un
enfoque físico clásico.
Teoría especulativa
Solamente a modo de conjetura
quisiera hacer un aporte más.
Un efecto similar al expuesto podría ser usando un imán sobre una chapa
metálica, de tal manera que se genere por la Ley de Lenz una repulsión y el objeto
flote.Rcuerde que la superficie de la tierra y el agua pueden ser consideradas conductoras
eléctricas. Pero claro, es un efecto como dije "similar" puesto que no
implicaría cambio de densidad de la materia sustentatora sino por repulsión magnética.
Me pregunto entonces si se pudiera realizar una nave en forma de disco a modo frisbee,
que gire sobre sí misma no su fuselaje material sino un dominio de campo de fuerza, tal
vez eléctrico, magnético, electromagnético o gravitatorio si se me permite. Este
pensamiento, como el lector notará, está orientado a indicar que semejante efecto
podría, quizá, aumentar la densidad del medio en que flota (agua, aire, atmósfera,
etc.) para lograr la levitación; o en su opuesto, disminuir el suyo logrando el mismo
efecto.
Apéndices
El efecto giroscópico
El giróscopo se destaca por cuatro funcionalidades: la precesión
("pre-cesar" o "movimiento antes de detenerse"), su cabeceo
(o nutación) al precesar, u antigravedad (levitación) y el
comportamiento de nutación.
Serán conocidos los tres experimentos básicos que nos ha dejado el ingeniero Eric Laithwaite
en su video. Al que posee el disco y
barral nos proponemos estudiar. La figura adjunta lo muestra.
El comportamiento de precesión
estará dado por lo siguiente:
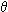 > precesión
("pre-cesar" o "antes de parar") > precesión
("pre-cesar" o "antes de parar")
Lfinal> = Lx> + 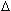 Ly> = Lf ( Ly> = Lf (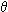 )> )>
 = = 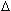 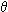 / / 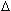 t
> velocidad de precesión (plano x-y) t
> velocidad de precesión (plano x-y)
tg 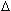 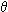 ~ ~ 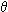 =
= 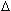 Ly / Lf Ly / Lf
 = = 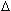 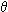 / dt ~ ( / dt ~ (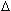 Ly
/ Lf) / Ly
/ Lf) / 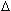 t = ( t = (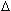 Ly / Ly / 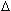 t) / Lf = Ty / Lf = r m g / J t) / Lf = Ty / Lf = r m g / J 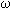 = 2
r g / R2 = 2
r g / R2  = =  ( (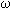 ) )
1 (arriba) > cos  = z / r > -1 (abajo) = z / r > -1 (abajo)
z = r cos ( - -  ) = z( ) = z( ) )
P = Pz  Ty Ty   Ly (si existe una F o P tendremos en cuadratura una L
generada) Ly (si existe una F o P tendremos en cuadratura una L
generada)
Lx  Tx Tx  Fz (si existe una L tendremos en
cuadratura una F que la genere) Fz (si existe una L tendremos en
cuadratura una F que la genere)
|