Son varios los motivos que explican la cuestión que
quiero abordar. Seguido las voy enumerando y explicando.
1º) Las Leyes de Faradary y Joule (Foucault)
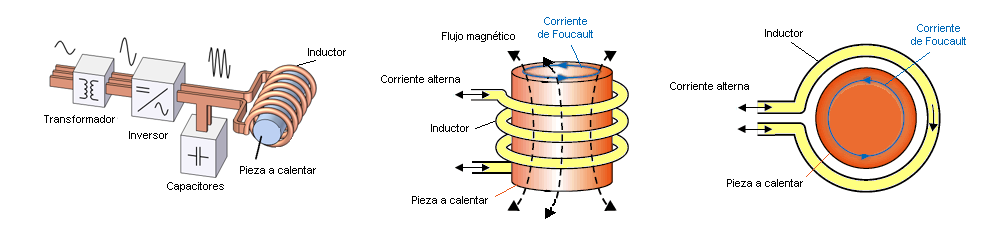
El flujo que produce el inductor del inversor inducirá por Faraday una tensión interna V
al material que dependerá de la velocidad del flujo  , eso ya es
conocido: V = d , eso ya es
conocido: V = d / dt / dt
Al usar un núcleo de hierro y debibo a su alta permeabilidad el flujo es alto y por
consiguiente también lo será la tensión inducida. Esto acarreará una alta corriente
por Foucault de calentamiento cuya potencia es P = V2/R = I2R,
siendo R la resistencia circular que ofrece el núcleo. Pero al utilizar aluminio o cobre,
este flujo es muchísimo menor y lo que se llega a calentar es mínimo, despreciable.
2º) El efecto pelicular (skin)
Todo material conductor que estará constituído por átomos, tendrán fijos sus núcleo y
algunos electrones en órbita, pero otros viajeros responsables del flujo eléctrico.
Así, estos últimos, generan a su derredor por la Ley de Amper debido a sus espines
asociados, un flujo magnético entre ellos que los separa. El efecto es que se
equidistancian unos de otros y la corriente tiende a ir acumulándose hacia la periferia
de material. Este efecto es concido como pelicular (skin) y dependerá,
obviamente y en forma inversa de la frecuencia, permeabilidad magnética y conductividad
del material. Dicho alejamiento de las paredes es exponencialmente natural y su
constante al 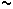 37% (1/e) se
la suele llamar "profundidad" (o "penetración") 37% (1/e) se
la suele llamar "profundidad" (o "penetración") 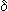 de la densidad de flujo eléctrico de la densidad de flujo eléctrico
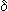 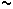 ( 2 / ( 2 / 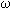 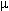 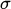 )1/2 )1/2
donde 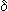 (m), (m), 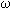 = 2 = 2 f (r/s), f (r/s), 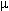 = permeabilidad magnética (Tm/A), = permeabilidad magnética (Tm/A), 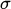 = conductividad
(S/m). Para los materiales que estamos analizando que son el hierro, el aluminio y el
cobre a una frecuencia típica de 100 kHz por ejemplo, resultan las penetraciónes
a temperatura ambiente respectivamente 0,02 mm, 0,28 mm y 0,20 mm. En otros términos el
primero se separa de los otros por una década de veces. = conductividad
(S/m). Para los materiales que estamos analizando que son el hierro, el aluminio y el
cobre a una frecuencia típica de 100 kHz por ejemplo, resultan las penetraciónes
a temperatura ambiente respectivamente 0,02 mm, 0,28 mm y 0,20 mm. En otros términos el
primero se separa de los otros por una década de veces.
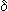 (mm) (mm) |
| |
Fe |
Al |
Cu |
| 1 kHz |
0,2 |
2,67 |
2,08 |
| 10 kHz |
0,08 |
0,84 |
0,66 |
| 100
kHz |
0,02 |
0,28 |
0,20 |
| 1 MHz |
0,008 |
0,08 |
0,08 |
| 10 MHz |
0,002 |
0,03 |
0,02 |
|
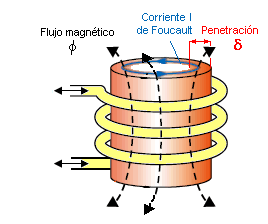
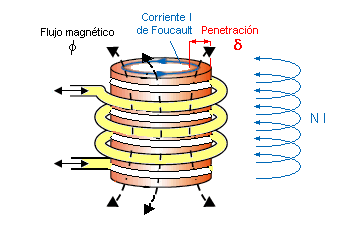
De esta manera, la
corriente de Foucault que llamamos I circulará no por todo el material céntrico del
cilindro-núcleo, sino con la profundidad 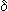 desde el borde de las paredes. El resto del material en el medio
enfriará lo poco que calienta esta circulación. desde el borde de las paredes. El resto del material en el medio
enfriará lo poco que calienta esta circulación.
|
|
|
3º) La necesidad de laminar
|
Centrándonos por
ejemplo en el aluminio, si lo laminamos en N chapas, obtendremos para cada una de éstas
la misma corriente I pero una total como suma de todas ellas que resultará NI, lo que nos
aumentará la potencia de calentamiento obtenida:
P = P1 + P2 + P3 +... = I2R
+ I2R + I2R = N. I2R
Si esta cantidad de láminas es lo suficientemente grande, podrá vencer el
enfriamiento del centro y conseguir que la pieza se caliente tomando una temperatura
requerida.
A su vez, el espesor de estas láminas yo la eligiría de por lo menos el ancho de
la penetrración 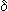 para
que no haya interacción. para
que no haya interacción.
|
|
|
4º) La Correlación cruzada
Este es un principio por mí bastante estudiado en sus aportes de la Física que puede ver
en este link.
Conclusión
Si se utiliza aluminio o cobre debidamente laminados y conectados en muchísimas capas,
entonces el calentamiento a inducción será perfectamente posible. Y estimo que más aún
que con el hierro. Esto revolucionaría la fabricación de los artefactos y ahorraría el
consumo las cocinas haciéndolas inclusive más pequeñas.
|