| |
|
INICIO
> ESCEPTICISMO DE HUME
|
|
Este es un tema que ya he tratado en mi libro
"Filosofía Crítica
Trascendental, Cap. 06, § De Hume a Kant-Laplace, y regreso a
Aristóteles", pero que ahora con estudios recientes he ampliado y quiero compartir.
Este contenido se ha ampliado en el siguiente enlace.
Introducción general
Fruto de una cultura occidental y empirista, la gnoseología de Hume trató a las ideas
cognitivas como fruto de la estructuración cerebral dada únicamente por las percepciones
sensoriales. Esto es decir que los conocimientos aquí no son sino ideas forjadas
de la percepción sensible, de la fenomenología espacio-tiempo. Esto determinó una
lógica agnóstica de la ley de la causalidad, puesto que la misma enlaza a las
causas y sus efectos pero que no puede ser conocimiento. No es fruto del tiempo-espacio.
Esto se conoció como escepticismo de Hume.
Aquí deseo frenar y comentar algo. Me refiero al significado del vocablo y concepto de
"conocimiento". En mi libro "Filosofía Crítica Trascendental" he relacionado el mismo al
vocablo "trascendental", y esto porque Immanuel Kant lo ha considerado
primero como un "conocimiento de las condiciones de la posibilidad" de
algo; esto es, que lo que conocemos es el mismo aspecto, o bien sinónimo, de lo
que "sentimos" como dado por sus posibilidades. Y este sentir
interno, otorgado por la percepción sensible (PES) y la extrasensible
(PES), en este estudio es aplicado sólo al primero.
Dicho en términos más sencillos, sólo podemos captar con nuestra sensibilidad las
entradas y salidas de un sistema causal, pero no al sistema en sí porque éste no
transcurre ni se espacializa con carácter fenomenológico. Por eso nos dice Hume
escépticamente: nada de lo que hay en el efecto me dice algo de su causa, sino sólo el
hábito ---aprendizaje neurofisiológico.
Así, todas las fenomenologías podemos llevarlas a funciones
matemática-físicas cognoscibles:

que para simplificar nuestro análisis y explicación solamente consideraremos la variable
tiempo 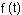 . .
Dicha postura ha sido superada (no solucionada) por
Kant y Laplace, que entiendo se contactaron por vías escritas, y resolvieron el efecto de
una misma manera pero a dos voces diferentes: el primero a través de los principios de
razón (filosofía) y el otro con la física (matemática). Ambos propusieron un cambio de
variable: no usar el tiempo-espacio sino la frecuencia, y se analizaría entonces esta
cuestión desde una manera espectral. Se conocería esto como convolución
laplaciana.
Preocupado Kant entre otras tantas cosas por la postura escéptica de Hume, decide
proponer una solución. En su obra cumbre Crítica de la razón pura dice que la
ley de causa-efecto es algo que uno trae a priori, es decir, desde el nacimiento,
y que le permite a uno formalizar al fenómeno en una ley. Es decir que, si bien esta no
se halla a ciencia cierta en la Naturaleza exterior a uno, sí empero se encuentra en la
Naturaleza interior. Más tarde fuera Schopenhauer quien la determinara como
característica cognitiva del proceso cerebral. Esta historia empero no termina aquí.
Sabemos que Kant mantenía correspondencia con Laplace y, no debiera ser casual entonces,
que exponga los conceptos de la convolución laplaciana. Seguidamente exponemos
el párrafo(1):
"Se trata, pues, de ver cómo una cosa [...] Todo cambio es, pues, posible sólo
por una acción continua de la causalidad, que en tanto que es uniforme se llama momento.
El cambio no se compone de estos momentos, sino que resulta como su efecto. Tal es la ley
de la continuidad de todo cambio. El principio de esta ley es: Ni el Tiempo ni el
fenómeno en el Tiempo, se componen de partes que sean las más pequeñas posibles, y sin
embargo, la cosa en su cambio no llega a su segundo estado sino pasando por todas estas
partes como por otros tantos elementos. [...] innecesario explicar cómo es posible. [...]"
y que comparamos a continuación con la fórmula de la convolución laplaciana
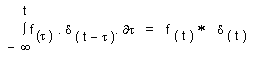
Así las cosas, las cuerdas de la guitarra producen un timbre en tiempo-espacio, aunque
podemos analizar su cuestión como armónicos. Este método no es sino una técnica abstracta,
una ideación cognitiva. Dicho de otra manera, la ley de la causalidad se entiende pensándola
pero no conociéndola puesto que no es fenómeno.
Se dirá sencillamente a Hume que tendría razón y que la fenomenología de la causalidad
en el tiempo-espacio no se la puede conocer, pero eso no nos
impide de que la podamos pensar (abstracción
cognitiva), como solución del primero.
Así, todas las leyes causales podemos llevarlas a funcionales
matemáticas (funciones de distribución) y no son cognoscibles aunque
sí pensables:
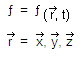
que para simplificar nuestro análisis y explicación solamente consideraremos la variable
tiempo 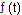 . .
Aquí quiero salvar, explicar una cuestión. Mucha gente dice entender las
cuestiones abstractas, pero, en realidad, las categorías del entendimiento que podrán
ser a priori (genéticas o hereditarias) o a posteriori (adquiridas)
desde el nacimiento, sólo permiten indagar su propia especificidad. Por ejemplo, no
podríamos entender a priori las fenomenologías porque ello se suceden luego del
nacimiento, pero sí estaremos preparados para sus entender nociones abstractas una vez
formadas en nuestro intelecto. Por todo esto, entender la convolución laplaciana
como fundamento superador del escepticismo de Hume no se podrá desde la mira
fenoménica, es decir, desde el esfuerzo de comprensión de la ley de causalidad
como algo espacio-temporal. No será asequible. Sólo podrá asimilarse desde el enfoque
de la abstracción espectral.
La convolución
Este concepto matemático no dista de su comprensión física.
Se realizará el producto de convolución de dos funciones: f (t) 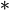 g (t) = y
(t). Tenemos dos maneras de explicar esto: una primera, considerando a g (t) como la transferencia
temporal (respuesta al impulso) ante la excitación para obtener la salida;
y otra segunda donde simplemente son funciones matemáticas.
g (t) = y
(t). Tenemos dos maneras de explicar esto: una primera, considerando a g (t) como la transferencia
temporal (respuesta al impulso) ante la excitación para obtener la salida;
y otra segunda donde simplemente son funciones matemáticas.
Considerando a g (t) como la respuesta al impulso
Las siguientes gráficas pretenden ser ilustrativas. Dado un sistema causalístico
que posee una excitación causal f (t) a su entrada
determinará una cierta salida
y (t) como efecto. Bien, como el dibujo muestra, hemos
considerado a esta primera como suma de impulsos de colores; cada uno de ellos aparecerá
a la salida sumándose en cierto instante t conforme la respuesta al impulso g (t -  ) que posea el sistema. De esta manera
la señal total y(t) será la suma de todos los aportes impulsionales. ) que posea el sistema. De esta manera
la señal total y(t) será la suma de todos los aportes impulsionales.
yk (t) = Area. g (t-k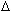  ) = f (k ) = f (k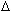  ). ). 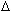  . g (t-k . g (t-k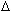  ) = ) =
n
n
y* (t) = 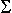 yk
(t) = yk
(t) = 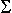 f (k f (k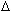  ). ). 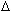  . g (t-k . g (t-k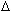  ) )
k=1
k=1
t
t
y (t) = lím y* (t) = g (t) 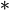 f (t) = f (t) =  g (t - g (t -  ) f ( ) f ( ) )   = =
 f (t - f (t -  ) g ( ) g ( ) )  
n 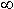 0
0
0
0
 |
|
|
|
Considerando a g (t) como una simple función matemática
De una manera general y no necesariamente para un sistema causal, la convolución
de dos funciones se define como la integral del producto de ambas (área) después de
desplazar a una de ellas cierta "distancia" (t -  ). ).
Aquí g (t) es el funcional (función de distribución)
que se aplica a la función de prueba (o de test) f (t)
( g (t) , f (t) ) =  g* (t) f (t) g* (t) f (t)  x x
Así y sencillamente, la convolución nos
dice que el fenómeno observado del presente es la suma de los resultados del pasado,
momento a momento dados.
Ejemplos ilustrativos
Para explicar con mayor claridad el tema, nos vamos a sumergir en una serie de ejemplos.
Se deberá recordar lo que es la transferencia espectral T(s) de
un sistema. Ella es el cociente salida a su entrada en la variable espectral compleja s =  + j + j 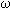 , y su anti-transformación por Laplace implicará la respuesta
al impulso , y su anti-transformación por Laplace implicará la respuesta
al impulso 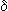 (0)
(que aquí denominamos transferencia temporal g (t)). Esto se debe a que si la
excitación es un impulso su espectro es constante y unitario, determinando un espectro a
la salida con la misma forma que la transferencia espectral. En suma: (0)
(que aquí denominamos transferencia temporal g (t)). Esto se debe a que si la
excitación es un impulso su espectro es constante y unitario, determinando un espectro a
la salida con la misma forma que la transferencia espectral. En suma:
T(s) = y(s) / f (s) =  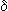 (0) (0)
1º) Sea un sistema que tenga una transferencia unitaria, es decir, que deje
pasar toda entrada sin deformarla, y que a su vez le aplicamos una señal en rampa
(triangular)
2º) Sea un sistema que tenga una transferencia inercial real de un solo
polo, y que a su vez le aplicamos una señal cuadrada
2º) Sea un sistema que tenga una transferencia pasabajos teórica, y que a
su vez le aplicamos una señal cuadrada. Por la transformación de Fourier tenemos el
espectro siguiente
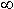 1/2
1/2
T(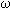 ) = ) =  g (t) exp -j g (t) exp -j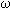 t t
 t = t =  1. exp -j 1. exp -j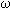 t t  t = 1. ( sen t = 1. ( sen 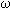 T/2 )
/ T/2 )
/ 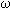 T/2 T/2
-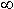 -1/2
-1/2
|
|
|
|
determinándonos una salida
|
|
Conclusiones
De la consideración precedente,
el tema escéptico pareciera pasar por querer conocer
la transferencia temporal g (t -  )
que "contiene" a ambos dominios temporales: tanto a "t" como a " )
que "contiene" a ambos dominios temporales: tanto a "t" como a " ", y restándolos. Sólo en el
espectro a través de la transformación de Laplace se unifica la proporcionalidad y(s) =
f(s).T(s), con ", y restándolos. Sólo en el
espectro a través de la transformación de Laplace se unifica la proporcionalidad y(s) =
f(s).T(s), con
T(s) =  g (t), puesto que la variable
compleja "s" ( g (t), puesto que la variable
compleja "s" ( +
j +
j 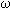 ) es común tanto para
"y" como para "f" y por tanto la podemos pensar
en un mismo momento. Sea tal vez que nuestra neurología "colapse" cuando
queremos que procese de una manera consciente (no así inconsciente como vemos en mi
otro estudio sobre el saludo)
informaciones en tiempos diferentes. ) es común tanto para
"y" como para "f" y por tanto la podemos pensar
en un mismo momento. Sea tal vez que nuestra neurología "colapse" cuando
queremos que procese de una manera consciente (no así inconsciente como vemos en mi
otro estudio sobre el saludo)
informaciones en tiempos diferentes.
Así las cosas y como afirmó Hume, no podemos tener conocimiento
sobre el enlazamiento de los efectos con sus causas, pero sí podemos pensar
en ello con abstracciones; ejemplo de ello lo son el dominio
espectral, la transformación z, los espacios abstractos de la mecánica cuántica, etc. |
|
|
Eugenio
Año 2000 al 23/10/14. Actualización del 28/12/25
Contacto, Mar del Plata,
Argentina |
| |
| |
Bibliografía
(1) KANT, Immanuel: Crítica de la Razón pura,
trad. por José del Perojo, rev. por Ansgar Klein, 5a ed., Bs. As., Losada, s/f, pp.
336-337 (A 212-213 y B 259-260)
(2) TAIT, Eugenio: Filosofía Crítica Trascendental,
Cap. 06, URL: http://eugeniotait.info/filosofiact
(3) HUME, David: Tratado de la naturaleza humana (1739),
Madrid, Orbis Hyspamérica, 1984, LIBRO I, INTRODUCCIÓN, # XX, p. 81.
(4) HUME, David: Investigación sobre el Entendimiento Humano
(1748), trad. por Francisco Romero, Bs. As., Losada, s/f, SECCIÓN CUARTA, PRIMERA PARTE,
p. 68; SECCIÓN SÉPTIMA, SEGUNDA PARTE, pp. 118-120
(5) Wikipedia
|
|
|
|