Dados los ejemplos que se habrán visto en los videos de este link, trataremos de aproximar magnitudes conforme al Video 1 de Firmat
|
v 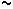 10 m/s 10 m/s
 velocidad del viento velocidad del viento
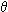 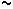 kt kt
 ángulo a la vertical
(< 10º) ángulo a la vertical
(< 10º)
k  constante constante
 = =  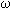 / / t = 2 t = 2 k/T. sen kt k/T. sen kt  aceleración angular aceleración angular
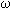 = 2 = 2 /T. cos /T. cos 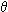 = 2 = 2 /T. cos kt /T. cos kt  velocidad angular velocidad angular
L 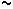 1,75 m 1,75 m  longitud de la
cadena longitud de la
cadena
g = 9,8 m/s2  aceleración de la
gravedad aceleración de la
gravedad
S 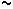 900 cm2 900 cm2
 mitad de la
superficie cóncava mitad de la
superficie cóncava
T 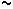 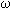  (L/g) = 2,65 s (L/g) = 2,65 s
 período oscilacion período oscilacion
Podremos determinar aproximadamente la fuerza F que se ejerce sobre una superficie
vertical S considerando un viento perpendicular v con una densidad típica del aire de
1,29 kg/m3, y con ello la presión P sobre la hamaca (me he valido de la ayuda
de la siguiente ref)
P = F/S = 5,81N / 900cm2 = 5,2 kg / 900 cm2 = 5,77 g/cm2 = 5,2
kg/hamaca  presión sobre la
mitad S de la superficie cóncava presión sobre la
mitad S de la superficie cóncava
Seguido también podremos estimar si se posee una oscilación normal sin influencia
externa. Para ellos de las ecuaciones generales de un péndulo simple se tendrá que
dar que L  g. O sea que si
hallamos g. O sea que si
hallamos
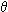 máx máx 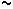 10º 10º  0,174 r
= k.T/4 = k. 0,662 s 0,174 r
= k.T/4 = k. 0,662 s
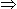 k =
0,263 r/s k =
0,263 r/s
resulta finalmente
L.  máx = L. 2 máx = L. 2 /T = 7,67 m/s2 /T = 7,67 m/s2
O sea que, salvando las aproximaciones hechas, podríamos decir que para ángulos
pequeños tenemos una oscilación T sin influencia externa puesto que las magnitudes más
o menos se corresponden (7,67 m/s2 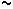 g), y que la
fuerza por hamaca para un viento sobrio está dentro del kg lo que producirá un
desplazamiento de la misma. g), y que la
fuerza por hamaca para un viento sobrio está dentro del kg lo que producirá un
desplazamiento de la misma. |

|
|
|
|
|