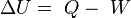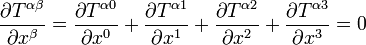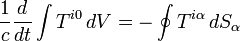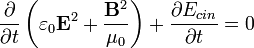Conservación de la energía

Sistema mecánico en el cual se conserva la energía, para choque perfectamente elástico y ausencia de rozamiento.

La ley de la conservación de la energía afirma que la cantidad total de energía en cualquier sistema físico aislado (sin interacción con ningún otro sistema) permanece invariable con el tiempo, aunque dicha energía puede transformarse en otra forma de energía. En resumen, la ley de la conservación de la energía afirma que la energía no puede crearse ni destruirse, sólo se puede cambiar de una forma a otra, por ejemplo, cuando la energía eléctrica se transforma en energía calorífica en un calefactor.

En termodinámica, constituye el primer principio de la termodinámica (la primera ley de la termodinámica).

En mecánica analítica, puede demostrarse que el principio de conservación de la energía es una consecuencia de que la dinámica de evolución de los sistemas está regida por las mismas características en cada instante del tiempo. Eso conduce a que la "traslación" temporal sea una simetría que deja invariante las ecuaciones de evolución del sistema, por lo que el teorema de Noether lleva a que existe una magnitud conservada, la energía.

Conservación de la energía y termodinámica

Dentro de los sistemas termodinámicos, una consecuencia de la ley de conservación de la energía es la llamada primera ley de la termodinámica, la cual establece que, al suministrar una determinada cantidad de calor (Q) a un sistema, esta cantidad de energía será igual a la diferencia del incremento de la energía interna del sistema (ΔU) menos el trabajo (W) efectuado por el sistema sobre sus alrededores:

$\Delta U = \ Q - \ W$

(ver Criterio de signos termodinámico)

Aunque la energía no se pierde, se degrada de acuerdo con la segunda ley de la termodinámica. En un proceso irreversible, la entropía de un sistema aislado aumenta y no es posible devolverlo al estado termodinámico físico anterior. Así un sistema físico aislado puede cambiar su estado a otro con la misma energía pero con dicha energía en una forma menos aprovechable. Por ejemplo, un movimiento con fricción es un proceso irreversible por el cual se convierte energía mecánica en energía térmica. Esa energía térmica no puede convertirse en su totalidad en energía mecánica de nuevo ya que, como el proceso opuesto no es espontáneo, es necesario aportar energía extra para que se produzca en el sentido contrario.

Desde un punto de vista cotidiano, las máquinas y los procesos desarrollados por el hombre funcionan con un rendimiento menor al 100%, lo que se traduce en pérdidas de energía y por lo tanto también de recursos económicos o materiales. Como se decía anteriormente, esto no debe interpretarse como un incumplimiento del principio enunciado sino como una transformación "irremediable" de la energía.

Véanse también: Móvil perpetuo y Rendimiento térmico.

El principio en mecánica clásica

• En mecánica lagrangiana la conservación de la energía es una consecuencia del teorema de Noether cuando el lagrangiano no depende explícitamente del tiempo. El teorema de Noether asegura que cuando se tiene un lagrangiano independiente del tiempo, y por tanto, existe un grupo uniparamétrico de traslaciones temporales o simetría, puede construirse una magnitud formada a partir del lagrangiano que permanece constante a lo largo de la evolución temporal del sistema, esa magnitud es conocida como hamiltoniano del sistema. Si además, la energía cinética es una función sólo del cuadrado de las velocidades generalizadas (o lo que es equivalente a que los vínculos en el sistema sean esclerónomos, o sea, independientes del tiempo), puede demostrarse que el hamiltoniano en ese caso coincide con la energía mecánica del sistema, que en tal caso se conserva.

• En mecánica newtoniana el principio de conservación de la energía, no puede derivarse de un principio tan elegante como el teorema de Noether, pero puede comprobarse directamente para ciertos sistemas simples de partículas en el caso de que todas las fuerzas deriven de un potencial, el caso más simple es el de un sistema de partículas puntuales que interactúan a distancia de modo instantáneo.

Véase también: Teorema de la energía cinética

El principio en mecánica relativista

Una primera dificultad para generalizar la ley de conservación de la energía de la mecánica clásica a la teoría de la relatividad está en que en mecánica relativista no podemos distinguir adecuadamente entre masa y energía. Así de acuerdo con esta teoría, la sola presencia de un partícula material de masa m en reposo respecto de un observador implica que dicho observador medirá una cantidad de energía asociadada a ella dada por E = mc². Otro hecho experimental contrastado es que en la teoría de la relatividad no es posible formular una ley de conservación de la masa análoga a la que existe en mecánica clásica, ya que esta no se conserva. Así aunque en mecánica relativista no existan leyes de conservación separadas para la energía no asociada a la masa y para la masa, sin embargo, sí es posible formular una ley de conservación "masa-energía" o energía total.

Dentro de la teoría de la relatividad especial, la materia puede representarse como un conjunto de campos materiales a partir de los cuales se forma el llamado tensor de energía-impulso total y la ley de conservación de la energía se expresa en relatividad especial, usando el convenio de sumación de Einstein, en la forma:

(1)$\frac{\part T^{\alpha\beta}}{\part x^\beta} =\frac{\part T^{\alpha 0}}{\part x^0}+ \frac{\part T^{\alpha 1}}{\part x^1}+\frac{\part T^{\alpha 2}}{\part x^2}+\frac{\part T^{\alpha 3}}{\part x^3}=0$

A partir de esta forma diferencial de la conservación de la energía, dadas las propiedades especiales del espacio-tiempo en teoría de la relatividad especial siempre conduce a una ley de conservación en forma integral. Esa integral representa precisamente una mangitud física que permanece invariable a lo largo de la evolución del sistema y es precisamente la energía. A partir de la expresión (1), escrita en términos de coordenadas galileanas 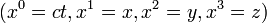$(x^0=ct,x^1=x,x^2=y,x^3=z)\;$, y usando el teorema de la divergencia tenemos:

(2)$\frac{1}{c}\frac{d}{dt}\int T^{i0}\,dV=-\oint T^{i\alpha}\,dS_\alpha$

Si la segunda integral que representa el flujo de energía y momentum se anula, como sucede por ejemplo si extendemos la integral a todo el espacio-tiempo para un sistema aislado llegamos a la conclusión de que el primer miembro de la expresión anterior permanece invariable durante el tiempo. Es decir:

(3)$\frac{d}{dt}P^i = 0, \qquad P^i := \frac{1}{c}\int T^{i0}\,dV$

La componente "temporal" 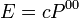$E = cP^{00}\,$ es precisamente la energía total del sistema, siendo las otras tres la componentes del momento lineal en las tres direcciones espaciales.

Conservación en presencia de campo electromagnético

En presencia de campos electromagnéticos la energía cinética total de las partículas cargadas no se conserva. Por otro lado a los campos eléctrico y magnético, por el hecho de ser entidades físicas que cambian en relación al tiempo según la dinámica propia de un lagrangiano, puede asignárseles una magnitud llamada energía electromagnética dada por una suma de cuadrados del módulo de ambos campos que satisface:

(4)$\frac{\partial}{\partial t} \left(\varepsilon_0\mathbf{E}^2+ \frac{\mathbf{B}^2}{\mu_0}\right)+ \frac{\partial E_{cin}}{\partial t} = 0$

El término encerrado en el primer paréntesis es precisamente la integral extendida a todo el espacio de la componente $T^{00}$, que de acuerdo con la sección precedente debe ser una magnitud conservada para un campo electromagnético adecuadamente confinado.

Véase también: Ley de Lenz

Conservación en presencia de campo gravitatorio

El campo gravitatorio dentro de la mecánica relativista es tratado dentro de la teoría general de la relatividad. Debido a las peculiaridades del campo gravitatorio tal como es tratado dentro de esta teoría, no existe una manera de construir una magnitud que represente la energía total conjunta de la materia y el espacio-tiempo que se conserve. La explicación intuitiva de este hecho es que debido a que un espacio-tiempo puede carecer de simetría temporal, hecho que se refleja en que no existen vectores de Killing temporales en dicho espacio, no puede hablarse de invariancia temporal de las ecuaciones de movimiento, al no existir un tiempo ajeno al propio tiempo coordenado del espacio-tiempo.

Otra de las consecuencias del tratamiento que hace la teoría de la relatividad general del espacio-tiempo es que no existe un tensor de energía-impulso bien definido. Aunque para ciertos sistemas de coordenadas puede construirse el llamado pseudotensor de energía-impulso, con propiedades similares a un tensor, pero que sólo puede definirse en sistemas de coordenadas que cumplen ciertas propiedades específicas.

Por otro lado, aún en la teoría de la relatividad general para cierto tipo de sistemas muy especiales, puede construirse una magnitud asimilable a la energía total del sistema. Un ejemplo de estos sistemas son los espacio-tiempos asintóticamente planos caracterizados por una estructura causal peculiar y ciertas condiciones técnicas muy restrictivas; estos sistemas son el equivalente en teoría de la relatividad de los sistemas aislados.

Finalmente cabe señalar, que dentro de algunas teorías alternativas a la relatividad general, como la teoría relativista de la gravitación de Logunov y Mestvirishvili, sí puede definirse unívocamente la energía total del sistema de materia. Esta teoría es totalmente equivalente a la teoría de la relatividad general en regiones desprovistas de materia, y predice desviaciones de la misma sólo en regiones ocupadas por materia. En particular la teoría de Logunov y Mestvirishvili, predice la no ocurrencia de agujeros negros, y esa es una de las principales predicciones que la diferencian de la teoría general de la relatividad de Albert Einstein.

El principio en mecánica cuántica

En mecánica cuántica aparecen algunas dificultades al considerar la cantidad de energía de un sistema a lo largo del tiempo. Así la energía total en ciertos sistemas aislados no está fijada para algunos estados cuánticos sino que puede fluctuar a lo largo del tiempo. Sólo los estados llamados estacionarios que son autovectores del operador hamiltoniano tienen una energía bien definida, cuando además el hamiltoniano no depende del tiempo.

Sin embargo, en sistemas aislados aún para estados no estacionarios, puede definirse una ley de conservación de la energía en términos de valores medios. De hecho para un sistema cuántico cualquiera el valor medio de la energía de un estado puro viene dado por:

(1)$\frac{d}{dt}\langle E \rangle_t = \langle \Psi(t) | \frac{\partial \hat{H}}{\partial t} | \Psi(t) \rangle$,

Y por tanto cuando el hamiltoniano no depende del tiempo, como sucede en un sistema aislado el valor esperado de la energía total se conserva. Aunque para algunos estados se observen fluctuaciones oscilantes de la energía cuya desviación estándar se relacionan con el principio de indeterminación de Heisenberg mediante:

(2)$\Delta E \cdot \Delta t \ge \frac{\hbar}{2}$,

donde: $\Delta E := \sqrt{\langle \Psi(t) | \hat{H}^2 | \Psi(t) \rangle - \langle E \rangle^2}$

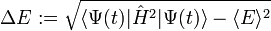
Véase también

• Termodinámica
• Energía
• Ley de conservación
• Criterio de signos termodinámico