Seguido explicaremos porqué los
cuerpos "caen". Es decir, demostraremos que la fuerza que se da en un objeto
hacia la Tierra en realidad es simplemente el efecto producido por su movimiento en el
espacio que ha sido deformado por la masa del planeta.
La siguiente demostración entiendo que es inédita porque corresponde a mi forma
de entender las cosas. Espero no estar en un error.
Demostración
que la masa contrae al espacio en su derredor
Nos enfocaremos especialmente en una masa M que es la de nuestro planeta Tierra.
Se sabe que dada la masa M = 5,97.1027 g del planeta Tierra y a un radio de su
centro R = 6,38.106 m que es el Ecuador, un objeto de masa m tendrá una aceleración de
gravedad g(R)=9,8 m/s2 en su caída libre. Este lo hará desde una altura yo
<< R que estará dada por las ecuaciones que siguen (puede recurrir a nuestro link) y la figura que las acompañan
Téngase en esto presente que si bien el tiempo del objeto se verá afectado por dos
cuestiones: la curvatura espacio-temporal que nos interesa y estamos estudiando, más la
expansión temporal debido a la corrección de Lorentz que despreciaremos debido a la baja
velocidad v de una caída libre frente a la de la luz.
Vemos que los espacios de la caída 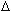 y se van contrayendo y sus tiempos y se van contrayendo y sus tiempos 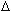 t
también manteniendo la fenomenología intrínseca (sin la masa M de perturbación) t
también manteniendo la fenomenología intrínseca (sin la masa M de perturbación)
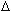 y1/ y1/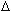 t1 < t1 < 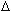 y2/ y2/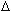 t2
< t2
< 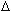 y3/ y3/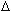 y3 y3
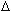 y1 > y1 > 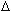 y2 > y2 > 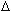 y3 y3
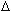 t1 > t1 > 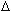 t2 > t2 > 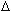 t3 t3
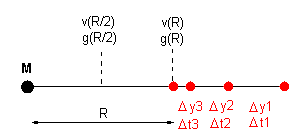
Por otra parte la aceleración de la gravedad va aumentando con el menor radio R (recordar
que 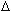 y << R); vea este dibujo que acompaña por
favor y << R); vea este dibujo que acompaña por
favor
| |
g(R/2) = GM / (R/2)2 =
4. g(R)  v (R/2) = 4. v(R) v (R/2) = 4. v(R)
(...)
g(R/n) = n2. g(R) ==> v(R/n) = n2. v(R)
|
|
|
o bien (vea este otro dibujo)
En suma, podemos decir que el espacio contraído que llamamos R´ vale (ver imagen)
R´ = R / n2
| n |
1 |
1,154 |
1,41 |
2 |
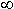 |
|
| R / n2 |
R/1 |
0,75R |
0,5R |
0,25R |
0R |
espacio sin la masa M |
| R´ |
R |
0,56R |
0,25R |
0,06R |
0 |
espacio con la masa M |
Se ha considerado hasta aquí una contracción del espacio dado por el factor 1/n2
para una masa M que es la del planeta Tierra.
| |
| |
| Explicación
del porqué los objetos "caen" |
|
| |
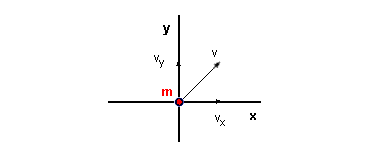
Nos valdremos de un espacio de
sólo dos dimensiones para simplificar y allí supondremos un objeto de masa m que se
encuentra viajando a una velocidad v como muestra la figura. Si lo descomponemos en sus
partes nos queda
v = [vx vy]T
|
|
|
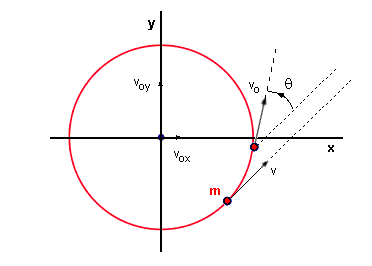
Ahora pensemos que dicho objeto se
encuentra girando en el perímero de una circunferencia donde su velocidad v es
tangencial. Al cabo de cierto tiempo habrá rotado un ángulo 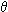 determinando con ello un nuevo vector que denominamos vo
que mantendrá su módulo y sus nuevos componentes son de una manera general los
siguientes y que han sido determinados por una matriz de rotación antihoraria R( determinando con ello un nuevo vector que denominamos vo
que mantendrá su módulo y sus nuevos componentes son de una manera general los
siguientes y que han sido determinados por una matriz de rotación antihoraria R(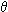 ) )
vo = [vox voy]T
R(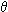 )
= [cos )
= [cos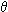 -sen -sen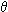 || sen || sen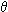 cos cos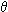 ] ]
resultando
vox = vx cos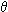 - vy sen - vy sen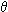
voy = vx sen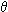 - vy cos - vy cos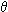
|
|
donde claramente se ve
que tienen componentes hacia el centro de la circunferencia y que van cambiando con el
avance de 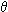 . . |
| |
Bien, si en el centro de la
circunferencia ponemos la masa M de la Tierra y es m un objeto apoyado en ella o bien
adherido en su atmósfera, estará por tanto girando a la velocidad de rotación terrestre
con un velocidad tangencial vo y sus componentes vox y voy
se hallan en dirección al centro del planeta.
Dicha velocidad del objeto es de un movimiento rectilíneo uniforme
(M.R.U.) y, por su principio inercial, seguirá la trayectoria del menor camino posible; y
esto es, debido a sus vectores vox y voy que puntan al centro
de la Tierra, a dicho punto central porque la masa M ha contraído su espacio en derredor
como hemos
demostrado precedentemente. Entonces se dice que "caen".
Así vemos que la denominada "fuerza de gravedad" no es ni más ni menos
que el destino al que converge el M.R.U. de una trayectoria debido a la contracción
espacial (comúnmente denominada "curvatura relativista") que ofrece una
masa M. |

|
|
Otra forma de entender
esto, más sencilla y conceptual tal vez, es que asumamos que así como existe un fuerza
centrífuga y velocidad potencial que impulsa al cuerpo hacia fuera, lo hay otra
igual y opuesta hacia dentro centrípreta en fuerza y velocidad potencial
también y que, debido a la contracción del espacio, se tiende al centro de la
Tierra. Un ejemplo utilizado comúnmente para ilustrar una órbita alrededor de un planeta
es el cañón
de Newton.
|
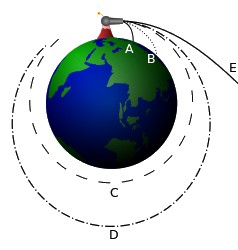
Se imagina un cañón
situado en lo alto de una montaña que dispara bolas de cañón de forma horizontal. La
montaña necesita ser muy alta para evitar la atmósfera terrestre e ignorar los efectos
de fricción sobre la bola de cañón.
Si el cañón dispara una bola con una velocidad inicial baja, la trayectoria de la bola
se curva e impacta contra el suelo (A). Aumentando la velocidad inicial, la bola de
cañón impacta en el suelo cada vez más lejos (B) del cañón, debido a que mientras la
bola sigue cayendo, el suelo también se curva. Todos estos movimientos son realmente
órbitas en su sentido técnico, ya que describen una trayectoria elíptica alrededor de
un centro de gravedad pero que se interrumpe al chocar contra la tierra.
|
Si se dispara la bola con
suficiente velocidad, el suelo se curva al menos tanto como la bola al caer, por lo que la
bola de cañón nunca impacta contra el suelo. Se dice que está realizando una órbita
sin interrupción o de circunnavegación. Para cada altura sobre el centro de gravedad hay
una velocidad específica que produce una órbita circular (C).
Si la velocidad de disparo aumenta más allá de esta velocidad, se producen órbitas
elípticas (D). A una velocidad mayor, denominada velocidad de escape, que de nuevo
depende de la altura donde se dispara, se produce una órbita infinita (E), primero del
tipo parabólica y con velocidades más altas del tipo hiperbólica. En ambos tipos de
órbitas infinitas el resultado es que el objeto ha escapado de la
gravedad del planeta y se marcha hacia el espacio. |
|
|
|