§ - El límite de una función

Cuando la causa x se "acerca" (valor acotado de antemano por nosotros) a una dada magnitud xo, decimos que la función y tiene por "límite" L que es una magnitud yo que le corresponde. Esto se expresa así

L =   Lím f(x)   =    Lím y
        x xo       x xo

Y no se puede encontrar L con un simple reemplazo de x=xo, puesto que hay funciones que son complicadas y no muestran el resultado directamente. Para comprender esto bastará un simple ejemplo. Sea el caso de querer hallar el L para cuando x=xo=1

y = (x² + 4x - 5) / (x - 1)

donde se pensará que (x - 1) = 0 y por tanto y = cosa que no es cierta en este ejemplo. Podemos ver esto si dividimos los polinomios porque resulta (x + 5) determinando y = 6

y = (x² + 4x - 5) / (x - 1) = x + 5 = 1 + 5 = 6

Para comprender mejor esto que ha ocurrido, separemos ambos polinomios y veamos cómo se acercan a xo

y y1 / y2

En otros términos, hemos logrado superar la "indeterminación" con el concepto de "límite", es decir, de cómo se van acercando a xo ambos polinomios que lo hallamos al dividirlos precedentemente

y = x + 5

§ - La derivada de una función

La "derivada" de algo es su "pendiente"; así de fácil.

Esta palabra implica que de una "función" y(x) se "deriva" (desprende) a otra función y´(x) que es la "pendiente" respecto a la abscisa x. Si y(x) tiene una unidad (magnitud), su y´(x) tendrá otra: la del cociente y/x; cuidado con eso.

En otros términos, punto a punto de esta y´ se está expresando un cociente de incrementos y/x que, yendo a un concepto puntual se escribe dy/dx como cociente de "incrementos infinitamente pequeños" que llamamos d, y esto no indica otra cosa que la tangente geométrica allí mismo

d 0 (adimensional, es un quantum) y´ = dy/dx = tg

A lo largo de la Historia se ha tenido distintos tipos de simbolgía que expresan lo mismo, veamos

- La de Leibnitz como dy/dx y su variante y/x para funciones de variables parciales como por ejemplo y=f(x,y,z)
- La de Lagrange como y´
- La de Euler como Dx
- La de Newton como
- La de la Física cuántica con incrementos cuánticos como y/x
- La mía (si se me permite) como y con =1/x un operador de función de distribución a la función y

Hay casos en que al encontrar la derivada nos da una función irracional indeterminada. Para superar esto se puede utilizar la Regla de L'Hopital que consiste en hallar el límite pero derivándola.

Para entender esta técnica, se puede pensar que la función original se halla compuesta por el cociente de otras dos funciones que llamaremos y1 e y2

y   y1 / y2

y con ello teniendo presente que los diferenciales son simplemente incrementos, logramos

L  =  Lím y  =  Lím y1/y2  =  d/dx . dx/d . Lím y1/y2   =  Lím y1´/y2´

o bien, expresándola con propiedad

L  =  Lím y    =   Lím y1´/y2´
        x xo     x xo


§ - La integral de una función

Historia

Aunque se basaron en ideas previas, se considera que la integral moderna fue ideada de forma independiente por:

Isaac Newton (Inglaterra, entre 1665 y 1666): Él desarrolló lo que llamó el "método de las fluxiones". Para Newton, la integración era el proceso inverso a la derivación (encontrar el área bajo una curva a partir de su velocidad de cambio). Curiosamente, no publicó sus hallazgos de inmediato por miedo a las críticas.

Gottfried Wilhelm Leibniz (Alemania, 1675): Desarrolló su propia versión de manera independiente. El 29 de octubre de 1675 es una fecha clave, ya que fue el día en que Leibnitz utilizó por primera vez el símbolo moderno de la integral ($\int$) en sus manuscritos. Como dato curioso tenemos que el símbolo "" es en realidad una "S" alargada que proviene de la palabra latina summa (suma), porque Leibnitz veía la integral como una suma infinita de rectángulos de ancho infinitesimal.

Mucho antes de Newton y Leibnitz, otros matemáticos ya daban los primeros pasos para calcular áreas curvas:

Arquímedes (287–212 a.C.): Es el precursor más importante. Utilizó el "método de exhaución" para calcular el área de un círculo y de una parábola, inscribiendo polígonos cada vez con más lados. Básicamente, estaba haciendo una integral sin tener el lenguaje del cálculo.

Bonaventura Cavalieri (1635): Poco antes de Newton, desarrolló el "método de los indivisibles", que trataba las áreas como si estuvieran compuestas por un número infinito de líneas paralelas.


1º Forma de explicación.

Su concepto, antagónico al del "incremento diferencial o infinitamente pequeño", es el de un "incremento infinitamente grande". Su símbolo es (adimensional, es un quantum también)

  = 

Podemos ver esto si pensamos

1    .0  =  .

o bien (que para esto podremos aplicar a un "álgebra de incrementos" sin ningún inconveniente)

= 1/

Al igual que un incremento diferencial podemos aplicarlo (afectarlo como producto, esto es contrayéndolo o expandiéndolo) a una variable como por ejemplo y, lo mismo será para la integral y pero, será "tan grande" y por lo tanto quedará indefinida, indeterminada porque su amplitud es infinita. Para poder implementar esto debemos acotarla, ponerle una limitación, y lo hacemos de la siguiente manera multiplicándola por un diferencial

y. x     yx y nos queda un área (indefinida por cierto), un producto de y.x (que tendrá esta unidad del producto), y debemos asimismo darle un entorno, una cota de mínimo a máximo que dispondremos entre x1 y x2 expresándolo finalmente de esta manera (integral definida) para que nos quede una superficie con límites racionales   x2 y. x = F(x2) - F(x1) = F(x) x1 o sea, hemos expresado en su concepto la denominada Regla de Barrow, que se demuestra también teniendo en cuenta que dicha F(x) siendo la función integral bajo la curva o dicho de otra manera que es la primitiva de la original y(x) F´(x) = y(x) y planteamos por ejemplo como hipótesis y que nos servirá para la demostración otra primitiva G(x) tal que, igual que antes, sea G´(x) = y(x)

Seguido y por otra parte, como sabemos que dos funciones que tienen la misma derivada se diferencian, a lo sumo en una constante k, resulta

G(x) = F(x) + k

por lo que si vamos al punto x=x1 resulta

G(x1) = F(x1) + k

pero como

              x1
G(x1) = y(x) x = 0
            x1
   0  =   F(x1) + k
   k  =   -F(x1)

con lo que la igualdad se convierte en

G(x1) = F(x) - F(x1)

y finalmente, si en esta última igualdad hacemos x=x2, obtenemos lo buscado restando las primitivas, que respetando al autor de esta demostración, se llama Regla de Barrow

                                      x1
F(x)  =  F(x2) - F(x1)  =  y(x) x
                                    x1

2º Forma de explicación. Sabemos con esto que la integral definida de la función representa el área F(x) que contiene como se ha mostrado. Bien, veamos otra manera de comprenderlo, quizá más conceptual por ser gráfica. De aquí el nombre de "integral" ("integración" de las partes constitutivas de la función). Para ello pensemos que la función y(x) se halla formada por infinitas muestras infinitesimales (x) como indica la figura, que tienen por base al infinitesimal x y abscisa la amplitud de la función y(x) en cada una de ellas. Podemos por lo tanto llegar al área F(x) mencionada si sumamos todas ellas             x2                                                                                                                   x2 F(x)  =   y(xi) x     =  y(x1). x   +   y(x1+x). x  +   y(x1+2x). x + ... =  y(x). x             x1                                                                                                                x1
3º Forma de explicación. Se quiere hallar el área de una figura cualquiera. Se ha elegido para generalizar la sencilla que se dibuja y(x) = x. Iremos ahora barriendo de izquierda a derecha con bastones verticales verdes formados por cuadrados de área 1, donde se observará que quedarán triángulos amarillos en la parte superior de magnitud 1/2. Ahora vamos observando que las áreas verde y amarilla van siguiendo la siguiente configuración que se dibuja siguiendo la función x2 / 2. Si relacionamos ambas funciones, pordremos ver con claridad que la primera es la función que deviene ("deriva") de esta segunda, resultando finalmente: f(x) = x = d(x2 / 2) / dx o bien x2 / 2 = f(x). dx
§ - La convolución de una función Así y sencillamente, la convolución nos dice que el fenómeno observado del presente es la suma de los resultados del pasado, momento a momento dados. Para ampliar este contenido puede ver el siguiente enlace.

El diferencial y la integral trascendentes

Cuando tenemos un incremento (o porcentaje) de un objeto, función, fenómeno o número, sabemos que podemos pensarlo como una fracción adimensional (sin magnitud) lo más pequeña que se nos ocurra: = 1/10, 1/100, 1/1000..., y cuando se llega a la indeterminación infinita deviene entonces el concepto de "diferencial" (que usaré con el símbolo de Jacobi para generalizar parcialidades de una función) = 1/.

De una manera antagónica, cuando este incremento adimensional aumenta, lo podremos llevar a un concepto extremadamente inmenso como el infinito: = 1/ = . En otros términos un diferencial es un incremento infinitamene pequeño y una integral no es sino más que un incremento infinitamente grande.

Estas fracciones, cuyas proporciones no tienen porqué ser idénticas, en la abstracción límite sí lo serán determinando por tanto que su producto es la unidad = 1


El operador trascendente

Lo que llamo operador trascendente no es más que el operador derivada de una función con la nomenclatura de Euler, entendida como funcional o función de distribución.

Es muy simple, no nos compliquemos. Observe cómo se aplica esto a una función cualquiera de una variable "x" usando la nomenclatura de Leibnitz

[ f(x) ] / x  =  D f(x)     anotación de una dervada con el operador "D" de Euler

Cuando estamos en Física, los conceptos de velocidad, aceleración, gradiente y laplaciano (divergencia del gradiente) toman, respectivamente y confome a mi nomenclatura (*¹), la siguiente disposición

[ f(t) ] / t  =  f(t)     anotación con mi operador trascendente de velocidad = /t
[ df(t) ] / t  =  ² f(t)      anotación con mi operador trascendente de aceleración ² = = /t = /t
[ f(x) ] / x  =  f(x)     anotación con mi operador trascendente de gradiente = /x
[ f(x) ] / x  =  f(x)     anotación con mi operador trascendente de laplaciano = /x ( /x)

Por consiguiente, estos operadores permitirán expresar funciones de distribución de un fenómeno f(x,t) dado. Esto es decir, funciones trascendentes que conformarán la distribución espacio-temporal de un cierto fenómeno.


La filosofía proposicional

Considerando a la Filosofía Proposicional del Lenguaje (*²), cada una de estas funciones de distribución implica un producto lógico, es decir, un adjetivo (predicado o cualificacón) aplicado a un sustantivo (sustancia, sustrato, objeto, fenómeno, cuantificación u ousía).

De esta manera vemos cómo es posible que un objeto, fenómeno o cosa física pueda ser adjetivizada, conformada, por una función trascendente. Y con ello, a partir de aquí, podemos establecer la existencia de un "álgebra de predicados", es decir, de poder operar estos funcionales con las propiedades del álgebra ortodoxa por todos conocida.

Así, sumarlos, restarlos, multiplicarlos, potenciarlos, pasarlos de un miembro a otro de una ecuación como términos, etc. se podrá hacer. Fíjese, a sólo modo de ejemplo, cómo podemos obtener fácilmente la ecuación de Euler-Lagrange (*³) con estos procederes:

L = Ecinetica - Epotencial    Lagrangiano
L  =  /. t/t. L = /t. t/. L = /t. L/(/t) = /t. (L/x)/(/t) = /t . L/x = L/x
  0  =  L - L  =  L/x - L    ecuación de Euler-Lagrange (/t. [L/(x/t)] - L/x)


Significado físico de los operadores

Sabemos que un incremento siempre lo es de algo, está o es un "sujeto" de algún "objeto".

De esta manera, si "simbolizamos" una cuestión esta puede ser perfectamente abstracta, es decir: un pensamiento. Pero cuando queremos "significar" algo, siempre hay una correspondencia ostensiva a un fenómeno u objeto fáctico, tal cual lo explica la semántica de la semiótica.

Para estos últimos casos, donde un operador trascendente que pretendemos se aplique o distribuya configurando a una función, entonces el mismo debe poseer un "significado". Por tanto, y para no alterar su contenido, lo hacemos con la unidad

    .1

de igual manera en la operativa integro-diferencial

    .1  = 1

y esto determina que los operadores trascendentes tienen la semejanza y propiedades de la función de Kronecker. Por ejemplo, cuando la variable es temporal, resulta

= /t   1/t       "muestreador impulsional", "impulso unidad" o "delta" de Kronecker *

o sea, posee un concepto muestral, que implicará una "muestra" temporal al fenómeno considerado distribuyéndolo (distribución o representación gráfica) y captando de él todo su contenido (fenomenología) desde el inicio hasta el final de los tiempos; esto es, que contedrá todo el fenómeno (*¹). Y esto resulta posible porque es una abstracción infinitamente aguda, o sea un impulso ideal cuyo espectro por tanto es infinito y plano de magnitud unitaria —por la transformación de Laplace. Su respuesta aplicada a un fenómeno (transferencia o transmitancia) determinará su contenido.

Es de notar que si la muestra f(t) —pendiente o velocidad en un punto del fenómeno f(t)— contiene la información de cómo ha fluído y de cómo lo hará, es evidente de que debe existir un potencial generatriz implícito en que informa dicho devenir. Llamo a esta nueva trascendencia , donde será por tanto =  ().

Los mismos conceptos podrán aplicarse a los demás operadores trascendentes, cobrando nuestra excusiva atención en nuestros estudios aplicados el del gradiente , donde haremos partícipe aquí también al nuevo concepto sugerido =  ().

Y finalmente para nuestra aplicabilidad trascendental (*¹) (respetando mi terminología original de hace décadas, aclaro que aquí "" no es ni un "incremento" ni un "laplaciano" sino un "operador trascendental de la fenomenología cuadrivectorial del espacio-tiempo") podemos generalizar () =  [ ()  () ]^T.


Los números complejos

Sabemos que en la Física del mundo hay magnitudes que son escalres y otras vectoriales (tienen dirección y sentido). Bien, muchas veces se precisa unir estas magnitudes, aunque no tengan las mismas unidades. Esto nos dará una cantidad complicada o "compleja", de allí el nombre. Ya no será un número sobre una recta, sino en un plano, un volumen, una multidimensionalidad, donde cada coordenada será "imaginada", de allí el nombre de número "imaginario".

Por convención, puesto que los cálculos se hacen más sencillos, se ha estipulado sumarlos como vectores en ortogonalidad. Pero siempre téngase presente, que el resultado es un mixto conceptual, no algo intrínsecamente válido. También y por convención, ajustado normalmente a realidades fácticas (no encuentro otra explicación), se suelen sumar en una misma recta como lo es el caso del espacio de Minkowski (usado en la Teoría de la Relatividad General), que es un espacio-tiempo plano con una métrica pseudo-riemanniana, donde se puede sumar un escalar y un vector utilizando la convención de hacerlo en una recta.

Pondré ejemplos que graficarán perfectamente lo que estamos diciendo:

1º- La Potencia aparente (medida en VA) de la Electrotecnia. Ella, será la suma vectorial ortogonal entre la Potencia activa (Watts) y la Potencia reactiva (VAReactivos o VAR). Este es un concepto energétio que involucra ampas energías, la calórica en el lugar y la de los campos eléctricos-magnéticos que se hagan allí también presentes. De tal manera esto es así, que el conocido "Principio de conservación de la energía" solamente es aplicable a la total aparente, y no a las demás (ver enlace explicativo).

2º- La Energía en un punto físico. Ella siempre está dada por 2 magnitudes: una escalar que proviene de la vibración atómica del material, es decir de su calor y que la medimos como temperatura, que podemos representar en Joules, y donde se suma a la posible energía activa de radiación electromagnética de onda plana que la atraviesa como vector de Poynting en Watts/m². Puede pensar como ejemplo en el principio de funcionamiento de un horno a microondas
doméstico. La resultante, sumada ortogonalmente también, será una totalista que no guarda una dirección y sentido, sino un concepto como la suma en cuadratura ortogonal de ambas. Un mixto.
Claro deberá estar que la energía total en el punto, fruto de la propia estática (potencial) que ya se dispone, sumada a la que le otorga la radiación (que no es cinética), será la suma no-ortogonal entre ellas, sino como en una simple recta lineal. Para lograr ello debemos unir las unidades, es decir, por ejemplo, tomar una superficie (y no un punto) y especificar el tiempo de ejecución. En este caso, ambas, la del punto (ahora una superficie) del material y la que nos llega como onda plana, estarán en Joules.

3º- La sensación térmica. Ésta, fruto de varias magnitudes como la temperatura del ambiente, la velocidad del viento, la humedad del lugar, la conductividad térmica del material, etc., producirán también un mixto totalista que se puede representar como un vector totalista que las contiene en ortogonalidad. Para hacer el ejemplo más sencillo, y aproximando, con sólo tener las dos primeras podemos obtener un resultado que bien podríamos llamar "enfriamiento".

También hay casos en que la cantidad de variables son muchas, y cuesta representarlas en abstracción mental, dejando solamente una aspiración de cometido de su comprensión. Éste bien podría ser el 4º caso que nombro a continuación:

4º- El espacio de Hilbert. Utilizado el concepto generalmente en la Física Cuántica para generalización del concepto del espacio euclídeo, suma bases (coordenadas funcionales de un espacio vectorial) combinadas ortogonalmente. Y de allí su difícil concepción. En el espacio de Hilbert, se utiliza una combinación de magnitudes escalares y vectoriales para describir el estado cuántico de un sistema. Los estados cuánticos se representan como vectores en un espacio de Hilbert, y se utilizan operadores lineales para transformar estos vectores y describir las interacciones entre el sistema y su entorno. Así, en este sentido, podríamos considerar que el espacio de Hilbert implica una forma de unidades mixtas, ya que combina magnitudes escalares y vectoriales para describir el estado cuántico de un sistema.

Y en cuanto a la otra aplicación, donde no hay números complejos y no se suman las magnitudes ortoganlmente, tedríamos el ejemplo que nombramos:

5º- La Métrica del espacio-tiempo de Minkowski. Aquí el espacio-tiempo de Minkowski es un espacio vectorial de cuatro dimensiones (tres espaciales + una temporal). Sus elementos se tratan como cuadrivectores (ct,x,y,z), y la diferencia entre dos eventos forma un vector. Lo que lo distingue es el producto interno: en lugar de la métrica euclídea positiva, usa la métrica de Minkowski (s² = -c²dt² + x² + y² + z²), que puede dar valores negativos, nulos o positivos. Así que vectores sí existen; lo que cambia es cómo se mide su “longitud”.
Por ejemplo, la energía total de un objeto se sabe que es E² = (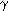mvc)² + (mc²)², donde 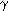es el Factor de Lorentz, m la masa, v la velocidad y c la velocidad de la luz. La expresión 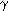mvc es la energía cinética (o momento) que es una magnitud vectorial, y mc² es la energía potencial que es una magnitud escalar. En resumen, la ecuación no representa una suma ortogonal en el sentido espacial tridimensional, sino una relación entre los componentes de un cuadrivector en el espacio-tiempo de Minkowski. Aquí, en este tipo de suma, las unidades deben ser las mismas.

6º- Asombrosamente, también se usan "ángulos complejos" en ciertas áreas de la matemática y física, como en la teoría de "Funciones complejas" (extender funciones trigonométricas a planos complejos), en "Transformaciones conformes".(mappings que preservan ángulos en planos complejos) o bien en "Física cuántica y ondas" (describir fenómenos ondulatorios con componentes complejos, como por ejemplo es la función tangente compleja: tan(z) = sin(z)/cos(z), con z = a + bi). Aquí un ángulo complejo es una extensión del concepto de ángulo real, utilizando números complejos. Se define como z = a + bi, donde "a" es el ángulo real y "b" es un componente imaginario que puede representar, por ejemplo, una rotación en un espacio más abstracto o una extensión analítica de funciones trigonométricas. Las funciones trigonométricas complejas correspondientes que los usan generalizan la geometría circular e hiperbólica, y corresponden, geométricamente, a un "Hiperboloide" (ref).


Referencias

(*¹)  TAIT, Eugenio Máximo - "Filosofía Crítica Trascendental" (2000), cap.1 Filosofía Crítica Trascendental, § Cálculo diferencial trascendental
(*²)  TAIT, Eugenio Máximo - "Epistemología y Lógica" (2000)
(*³)  Wikipedia - "Lagraniano", https://es.wikipedia.org/wiki/Lagrangiano