| |
|
INICIO
> LA PROBABILIDAD Y LA POTENCIA (FÍSICA CLÁSICA Y CUÁNTICA)
|
Aquí mostraremos que la Probabilidad y la Potencia son prácticamente una y la
misma cosa. Y más todavía, tienen semejanza también con los cuños de Poder,
Posibilidad y Potencial. Son estos cinco términos sino sinónimos aplicados a distintas
especificidades, es decir, a distintas disciplinas. Sus raíces etimológicas vienen de
Aristóteles. Revisemos primero lo que nos dicen de ellas el diccionario ortodoxo:
Potencia: El término potencia (Aristóteles)
es un concepto filosófico opuesto al de acto. Es la propiedad que tienen los
seres (desde el punto de vista metafísico) de recibir los accidentes que causan la
transformación de la sustancia. (ref)
Poder: El término poder se entiende como sinónimo de fuerza, capacidad,
energía o dominio. (ref)
Probabilidad: La probabilidad es un método por el cual se (puede
obtener) la frecuencia de un acontecimiento determinado mediante la realización de un
experimento aleatorio del que se conocen todos los resultados. (ref)
Posibilidad: Posible es todo aquello que puede
ser, que puede existir, que existe o que puede suceder. (ref)
Potencial: Potencial es una magnitud escalar definida en los campos
conservativos. Por ejemplo, el voltaje es considerado el potencial del campo eléctrico
porque lo generaría, lo puede configurar. (ref)
Para explicar y ampliar el tema, quiero compartir unas analogías que he encontrado.
Permítasenos presentar la cuestión desde un punto meramente conceptual.
Conceptos introductorios
Se conocerá el hecho que la Probabilidad P de hallar una partícula en
mecánica cuántica está dada por la ecuación siguiente
P =   x | x | (x)|2 (x)|2
y que permitirá hallar a la Densidad de la Probabilidad | (x)|2 como (x)|2 como
| (x)|2
= (x)|2
=  P/ P/ x = x =  P P
De una manera análoga, si disponemos de un resistor eléctrico R que configura
constante 1/k su magnitud a lo largo de su longitud x, y lo calentamos con una corriente
eficaz I determinará en él una Potencia P según la ecuación
I2 = P / R =  P/ P/ R = R =  P/ P/ R
. ( R
. ( x/ x/ x) = x) =  P/ P/ x . ( x . ( R/ R/ x)-1
= k . x)-1
= k .  P P
cosa que a su vez determinará la similitud con la ecuación hallada
precedentemente
Las propiedades de la indeterminación
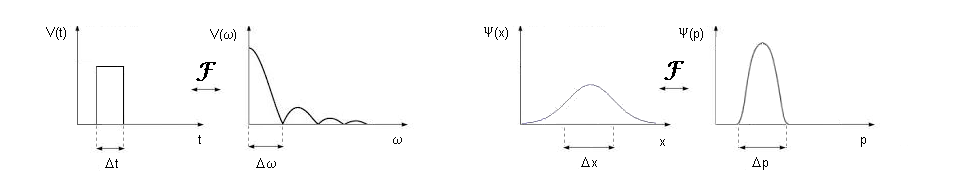
Cuando hablamos de electricidad, por ejemplo, una función de onda de voltaje que
transcurre en el tiempo V(t) (o bien de corriente I(t) como en la explicación anterior) y
que tendrá un contenido armónico de envolvente V(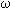 ) hallado por la Transformada de Fourier, para hablar de su
Poder usamos el concepto de la energía que dispone al expresar su Potencia como su valor
(eficaz) al cuadrado |V|2 que implica una Densidad. Recuérdese que ) hallado por la Transformada de Fourier, para hablar de su
Poder usamos el concepto de la energía que dispone al expresar su Potencia como su valor
(eficaz) al cuadrado |V|2 que implica una Densidad. Recuérdese que 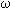 es la velocidad angular de cada
armónico. Si esta función V(t) es un impulso de duración es la velocidad angular de cada
armónico. Si esta función V(t) es un impulso de duración 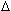 t implicará necesariamente un ancho
de banda (velocidad) aproximado de armónicas de magnitud t implicará necesariamente un ancho
de banda (velocidad) aproximado de armónicas de magnitud 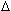 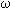 tal que su producto es constante tal que su producto es constante 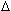 t. t.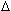 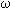 = cte. = cte.
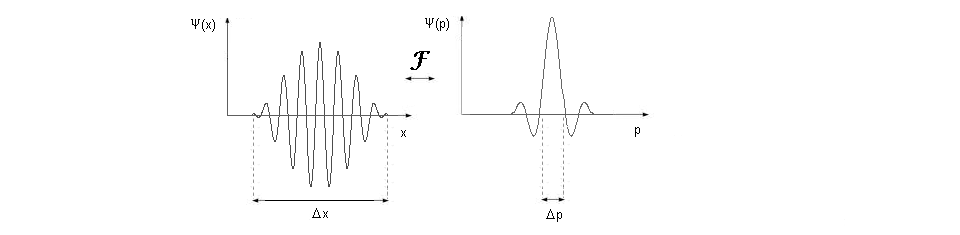
De similar manera y cuando hablamos de mecánica cuántica, por ejemplo para una
partícula en movimiento, hablamos de una función de onda que deviene en el espacio  (x) que tendrá una correspondencia (x) que tendrá una correspondencia  (p) hallada por la Transformada de
Fourier, y para hablar de su Poder usamos el concepto de Densidad de Probabilidad como su
magnitud al cuadrado | (p) hallada por la Transformada de
Fourier, y para hablar de su Poder usamos el concepto de Densidad de Probabilidad como su
magnitud al cuadrado | |2.
Recuérdese que p = m.v donde v es la velocidad. Si esta función |2.
Recuérdese que p = m.v donde v es la velocidad. Si esta función  (x) es una distribución de ancho (x) es una distribución de ancho 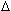 x implicará necesariamente una
amplitud aproximada de magnitud x implicará necesariamente una
amplitud aproximada de magnitud 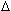 p
(velocidad) tal que su producto es constante. Aquí la indeterminación de Heisenberg: p
(velocidad) tal que su producto es constante. Aquí la indeterminación de Heisenberg: 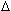 x. x.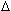 p = cte = p = cte = 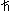 /2 /2
Otro tanto se obtiene cuando analizamos lo que se llama un "paquete de
ondas"  (x,t)
electromagnéticas propagadas. La misma, con la analogía cuántica (x,t)
electromagnéticas propagadas. La misma, con la analogía cuántica
k = p.2 / /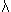 se obtiene por medio de la
Transformada de Fourier directa e inversa un espectro se obtiene por medio de la
Transformada de Fourier directa e inversa un espectro  (p) (p)
 (x,t) = (2 (x,t) = (2 )-1/2 )-1/2   p p  (p)
exp j(px - (p)
exp j(px - 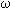 t) t)
 (p) = (2 (p) = (2 )-1/2 )-1/2   x x  (x,0)
exp -jpx (x,0)
exp -jpx
y que contiene un espacio 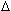 x
brindando un contenido armónico x
brindando un contenido armónico 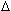 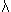 o su equivamente o su equivamente 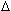 p al considerar la mecánica
cuántica. Esto se puede demostrar que brinda una indeterminación p al considerar la mecánica
cuántica. Esto se puede demostrar que brinda una indeterminación 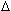 x. x.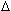 p p 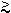 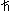 /2 /2
Las propiedades de la función de Dirac
La función de distribución 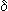 permitirá aplicarse como muestra de una función para
convolucionarla tanto en el tiempo como en el espacio: permitirá aplicarse como muestra de una función para
convolucionarla tanto en el tiempo como en el espacio:
V(t) =   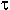 . V( . V(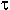 ) . ) .
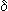 (t- (t-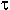 ) = V(t) ) = V(t) 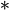 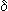 (t) (t)
 (x) = (x) =   r . r .  (r)
. (r)
. 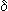 (x-r) = (x-r) =  (x) (x) 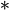 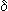 (x) (x)
Analogías experimentales
Hablemos ahora de los resultados obtenidos en la experiencia de Feynman de la doble
rendija y sus derivados. Para los lectores familiarizados con estos experimentos, las
siguientes imágenes muestran a las mismas con partículas, ondas de agua y luego
electrones. Vemos comprensible los resultados de la analogía entre la Probabilidad y la
Potencia que se obtienen; lo que ocurre es que cuando hay difracción (ondas) la cuestión
energética se comprende con la primera, y cuando no la hay porque son partículas, será
con la segunda.
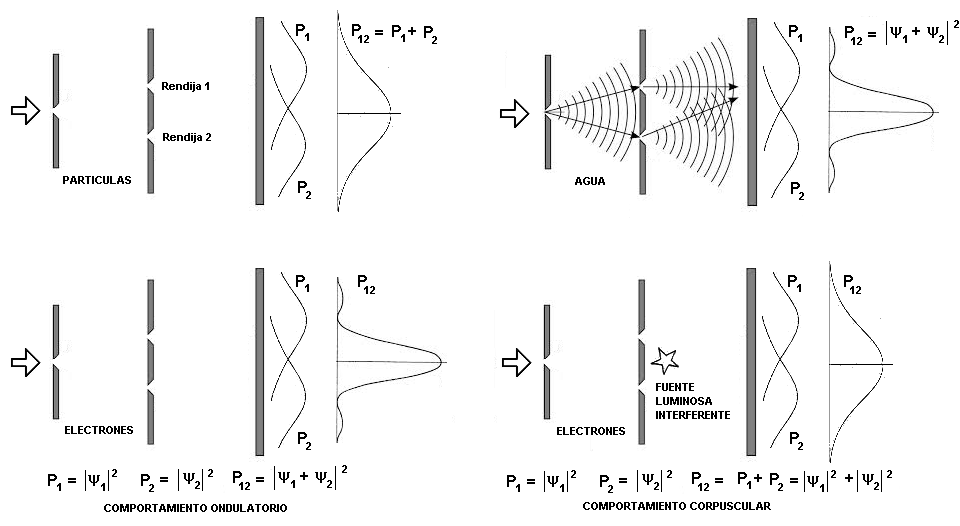
Donde se ha definido a la Probabilidad P y su Densidad de Probabilidad | |2 |2
P =
número de electrones que llegan / número de electrones que salen del cátodo
| |2
= |2
=  P/ P/ x x
Se pone en evidencia aquí que se trata a | | como un valor eficaz, similar al usado en la
técnica fasorial de la electrotécnica al dado valor pico | | como un valor eficaz, similar al usado en la
técnica fasorial de la electrotécnica al dado valor pico | > >
| | =
| | =
| > / > /
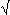 2 2
o sea que se dan las
correspondientes similitudes
Probabilidad = P12  | | 12|2 = | 12|2 = | 1|2 + | 1|2 + | 2|2 2|2  Comportamiento corpuscular Comportamiento corpuscular
Probabilidad = P12  | | 12|2 = | 12|2 = | 1 + 1 +  2 |2 2 |2  Comportamiento ondulatorio Comportamiento ondulatorio
Potencia = P12 = P1 + P2  | | 12|2
= | 12|2
= | 1|2
+ | 1|2
+ | 2|2 2|2
 Comportamiento
energético (suma de potencias) sin interacción (no correlacionadas) Comportamiento
energético (suma de potencias) sin interacción (no correlacionadas)
 Comportamiento corpuscular
Comportamiento corpuscular |
| |
|
Seguidamente compartimos otra experiencia, la
de una rendija con un haz electrónico. De la óptica clásica se sabe que la difracción
obtenida aquí es como la representada y donde se cumplen que 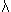 >> b y sen >> b y sen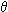 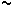 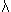 / b. Seguidamente y como se
considera una cantidad de movimiento p cuya acción transversal llamamos / b. Seguidamente y como se
considera una cantidad de movimiento p cuya acción transversal llamamos 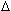 p, teniendo en cuenta a De
Broglie p, teniendo en cuenta a De
Broglie 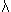 = h / p,
entonces se dan las sencillas ecuaciones que indican = h / p,
entonces se dan las sencillas ecuaciones que indican 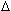 x. x.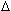 p
= h / 2 y que se acerca al concepto de la indeterminación de Heisenberg. En verdad, lo
que quiero compartir aquí no es ésta conclusión, sino el hecho de considerar para su
análisis, en un mismo momento temporal, las consideraciones ondulatorias y corpusculares;
como si se dieran ambas, repito, en el mismo instante. Esto es, como si los electrones
fuesen onda y partícula una misma cosa siempre, y no necesariamente desmembrándolo para
explicar una u otra cuestión física. p
= h / 2 y que se acerca al concepto de la indeterminación de Heisenberg. En verdad, lo
que quiero compartir aquí no es ésta conclusión, sino el hecho de considerar para su
análisis, en un mismo momento temporal, las consideraciones ondulatorias y corpusculares;
como si se dieran ambas, repito, en el mismo instante. Esto es, como si los electrones
fuesen onda y partícula una misma cosa siempre, y no necesariamente desmembrándolo para
explicar una u otra cuestión física.
|

|
Por otra parte y si se me permite, quisiera
expresar una hipótesis. Observo que el electrón pareciera que es una
partícula que viaja no "como" sino "en" una onda, que es uno y lo
otro en el mismo momento. Como si se montara sobre ella. Esta onda así entendida sería
generada por el mismo electrón y se autotransporta. Este concepto derribaría el
hecho de que el electrón se halle en ambas rendijas al mismo tiempo; es decir, que el
electrón pueda estar en dos lugares al mismo tiempo y el hecho de desdoblar su energía
pasaría a ser un error, una fantasía. El electrón pasa por ambas redijas
"subido", transportado por su misma onda e impacta sobre la placa final conforme
a su propia interferencia. Empero, de qué manera se da esto ubicándose el electrón
partícula en su propio frente de onda es un tema que aún no entiendo. Tal vez un avance
del tema los haya podido dilucidar en este link y que seguido
explicamos.
Una mira más sólida de las ecuaciones abordadas permitiría interpretar el efecto
de otra manera. Es como es como si el electrón tuviese dos entelequias que se
hallan correlacionadas (cuerdas quizá) —como puede ver más adelante. Cuando se lo observa, esto
es decir que se le quita energía en una mensura, será precisamente la energía de la
correlación y entonces el electrón de su estado natural ondulatorio pasa al
desnaturalizado que sería una partícula. Vista así las cosas, no es que exista
una dualidad onda-partícula, sino sólo una partícula (doble) ondulada que, al
ser afectada, queda incompleta y se muestra como partícula. Repito, en el
siguiente link se
explica mejor el efecto.
El mismo Feynman ha dicho que “Creo que puedo afirmar con seguridad que
nadie entiende la mecánica cuántica“. Bien, y aquí hay un punto en el cual
debemos detenernos: en lo que es el entendimiento. Esta es una facultad en el intelecto
como la capacidad que tiene la "mente" de una persona para discernir cómo se
relacionan entre sí las partes o aspectos de un asunto e integrarlas. En otros términos,
para aprehender algo, ya sea fenoménico o abstracto, deben darse categorías en
él que se homogeinizen con ese algo. El entender algo implicará tener una
categoría que le sea afín a la aprehensión dada. Dichas categorías pueden darse, a
partir del nacimiento, como fruto de la experiencia (adquiridas o a posteriori) o
bien ser genéticas (a priori). Por este motivo considero que la dificultad
planteada por la mecánica cuántica radica en una limitación biológica de nuestra
neurología, cuestión que tal vez logre superarse con la ayuda de la seria introspección
filosófica, aún con la misma filosofía del lenguaje si ésta se acuña como
fruto de una cosmovisión de lo que nos rodea. |
| |
| |
La
correlación cruzada
Vemos que el Comportamiento corpuscular del ondulatorio precedente se diferencian
por una correlación cruzada; esto es, posiblemente, fruto de una interacción
hamiltoniana. Entiendo que dicho concepto es análogo al que se aplica en la
electrotecnia.
Para poder comparar esto, pensemos en una implementación eléctrica como se
muestra en la figura. Un generador implementa sobre el circuito dos señales de corriente
continua Ia e Ib y que se hallarán correlacionadas: una aparecerá
luego de la otra, aplicadas sobre un resistor R configurando una total Iab.
Este efecto es como si fueran sistemas, es decir circuitos, totalmente separados uno del
otro.
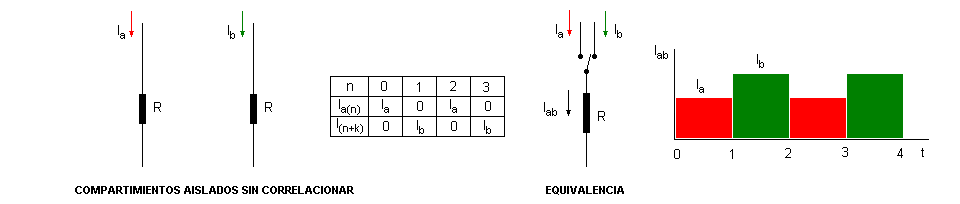
Aquí la correlación cruzada Cab entre ambas corrientes
valdrá
N-1
Cab = (1 / N) 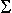 Ia(n) I(n+k) Ia(n) I(n+k)
n =0
donde N (= 4) es el número de elementos, n los períodos considerados y k (= 1) el
retraso. O se que si se me permite hablaré de una correlación cruzada normalizada
Cn
3
Cn = N Cab = 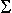 Ia(n) I(n+1)
= 2 Ia Ib Ia(n) I(n+1)
= 2 Ia Ib
n =0Seguidamente implementaremos otro segundo circuito que sume ambas
corrientes para hallar la Potencia P sobre el resistor normalizada a R
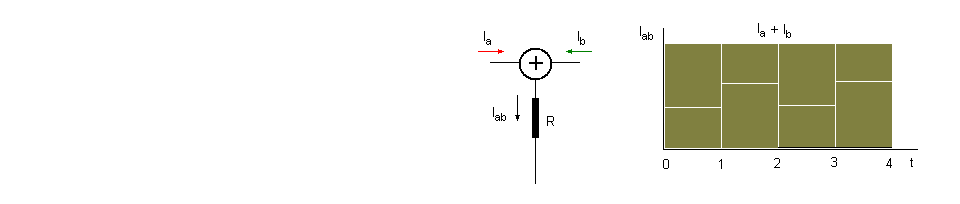
Iab = Ia+ Ib
P/R = Iab2 = ( Ia+ Ib
)2 = Ia2 + 2 Ia Ib
+ Ib2 = Ia2
+ Ib2 + Cn 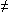 Ia2
+ Ib2 Ia2
+ Ib2
cuestión que pone en evidencia que el teorema de superposición de la
electrotecnia no es posible aplicarlo a las energías (Potencias) si no se corrige su
efecto con la correlación cruzada.
Bien, ahora si vamos a
las expresiones encontradas en las experiencias de la doble rendija observamos
perfectamente dos cosas: una primera, que para el caso de partículas se están
considerando efectos aislados y para la ondulatoria correlacionados (interacción
interferente); y segundo que se acentúa nuestra hipótesis de que los anáslisis para la
Probabilidad y para la Potencia son una y la misma cosa. En suma, para lo primero
tendríamos:
Comportamiento ondulatorio =
Comportamiento corpuscular + Correlación cruzada
Esta mira permitiría conjeturar que el paso del comportamiento
ondulatorio al corpuscular por la interferencia colapsadora viene dado por la afectación
o quite de la correlación cruzada.
|
| |
|
El clínamen
La experiencia de la doble rendija primero supone partículas sólidas arrojadas por un
proyectil, digamos, imperfecto. Su magra exactitud y precisión de certeza en el acierto a
la rendija determinará la estocástica que vemos como función de distribución en la
pantalla final. Bien, aquí habría entonces que hablar del clínamen.
Este es un concepto no tan sencillo sino que, permítasenos decir, "se las
trae". Es el nombre en latín que dio Lucrecio a la impredescible desviación que
sufren los átomos en la física de Epicuro ("declinación de los átomos").
Dicho concepto le sirvió al filósofo griego como modo de solución al problema del libre
albedrío
prescindiendo de un dios garante de libertad.
La teoría del clínamen proporciona una solución al viejo problema planteado
por Aristóteles de la regresión al infinito en las cadenas causales del movimiento, y
sin tener que recurrir a la acción de un dios ordenador que funcione como primer
motor inmóvil. Para solucionarlo se introdujo el clínamen, o desviación
espontánea del átomo de su trayectoria como origen de nuevas cadenas causales. Con ello,
se eliminaban a los dioses de la cadena de razonamientos a la vez que se introducía un
factor de indeterminación que solucionaba uno de los principales problemas del atomismo
democríteo: el determinismo. Es decir, el clínamen proporcionaba una
base ontológica sólida en la que justificar el libre albedrío. Ya que sin
libertad las acciones morales dejan de serlo, el clínamen se erigió también
como fundamento de toda posibilidad de una ética atea.
Conocemos la doctrina del clínamen a través del poeta y filósofo latín
Lucrecio, que en el Libro Segundo de su poema De Rerum Natura que dice: "(...)
cuando los átomos caen en línea recta a través del vacío en virtud de su propio peso,
en un momento indeterminado y en indeterminado lugar se desvían un poco, lo suficiente
para poder decir que su movimiento ha variado. Que si no declinaran los
principios, caerían todos hacia abajo cual gotas de lluvia, por el abismo del vacío, y
no se producirían entre ellos ni choques ni golpes; (y) así la Naturaleza nunca hubiera
creado nada."
La experiencia realizada, que supone hecha de a un electrón en vuelo en cada impacto en
la pantalla, si mis cálculos no están en un error, determinaría una corriente
eléctrica de magnitud del orden de los picoamperes
q = -1,602 .10-19 C (carga del electrón viajero)
L = 0,1 m (longitud del TRC estimada)
v = L/T = 10000 Km/s = 107 m/s (velocidad en el TRC estimada) (ref)
lo que nos da
T = L / v = 10-8 s (tiempo entre cada electrón)
I =  q/ q/ t = q/T = -1.602 .10-19 C /
10-8 s t = q/T = -1.602 .10-19 C /
10-8 s 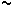 -16 pA (corriente de la circulación electrónica)
-16 pA (corriente de la circulación electrónica)
y que también entiendo supone una doctrina del clínamen.
Ahora bien, será fácil comprender un clínamen para el caso de un dispositivo
de emisión de partículas porque es mecánico, con pequeñas y esperadas fallas en sus
componentes; pero en el caso de emisión termoiónica acelerada por campo elécrico,
estático y continuo por la perfectibilidad de la tensión continua implementada, en
verdad, me deja dudas en cuanto a la aleatoriedad instrumentada.
De todas maneras se asegura, en el ámbito serio de la disciplina Física, que esto se ha
medido y hallado; entiendo que existe la referencia "Donati, O, Missiroli, G F,
Pozzi, G (1973). An Experiment on Electron Interference. American Journal of
Physics".
En suma, lo que quiero hacer notar es que este éfecto del clínamen se halla en
la experiencia cuántica onda-partícula y también, como segunda observación, que el
mismo es afectado cuando el experimento es perturbado ("observado" como
sabemos), esto es, como que la afección se ha realizado sobre el mismo clínamen.
No afirmaría, aunque tampoco tendría herramientas para negar, que el clínamen
entonces es causa originaria de las formas de distribución resultantes. |
| |
| |
|
Conservación de los Observables
Probabilidad y Potencia
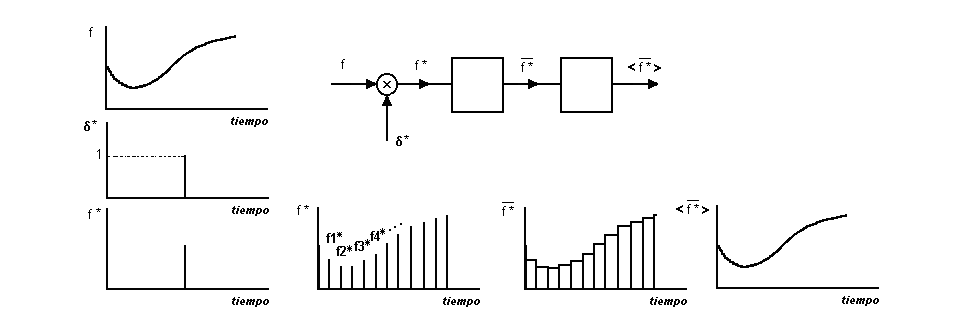
Sabemos que los Observables en la mecánica cuántica son aquellas mediciones que
se realizan en un instante dado; es to es decir, que son atemporales. Esto no significa
necesariamente que la acción "f" medida no evolucione temporalmente, sino que
se deberán tomar muestras de la misma en un instante dado, luego en otro, otro y así
sucesivamente. Estos continuos chequeos determinarán un continuo discreto; esto es, que
continuadas una tras otra no será de otra manera sino con una cuantidad constante
configurando una función escalonada, cada vez más continua cuanto más breves sean las
muestras, menos distanciadas en el tiempo lo estén unas de otras y mayor cantidad haya.
Esta manera de trabajar, para una partícula cargada sometida a una fuerza, entiendo que
se podrán determinar por ejemplo a los Observables asociados a la Probabilidad, así como
también si lo hacemos con la Energía y, por tanto, tendrá a su vez una correspondencia
con la Potencia. En suma, no veo dificultad para asociar un Observable a esta última.
Por esto y como se entederá, la conservación de la Probabilidad y de la
Energía en la mecánica cuántica, traerá aparejado esta última una conservación
también de la Potencia.
Ahora voy a analizar esto conceptualmente, omitiendo las razones vectoriales, con
una simbología abreviada a mi parecer y tomando las cuestiones lo más sencillamente
posible. Esto considerará lo siguiente:
- Espacio en una sola dimensión x
- Uso del operador delta de Dirac-Kronecker 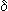 para abreviar al operador velocidad para abreviar al operador velocidad  / / t t
- Uso del operador nabla  para abreviar al operador
gradiente (o divergente) para abreviar al operador
gradiente (o divergente)  / / x x
- El símbolo integral  es un incremento infinito porque es la inversa del diferencial
es un incremento infinito porque es la inversa del diferencial  . O sea que . O sea que   .1 = 1 .1 = 1
De esta manera podría yo pensar, a disculpas de los verdaderos profesionales en Física
que comprenderán mucho mejor y con autoridad académica las cuestiones que yo seguramente
abuso, lo siguiente para el caso de una superficie cerrada que contenga un volúmen de
donde salga una densidad de corriente de partículas eléctricas J (ref 1, ref 2, ref 3):
Potencia = P =  <E(t)>/ <E(t)>/ t = t = 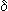 <E> = < <E> = < | | 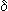 H | H | >
= constante >
= constante
Probabilidad = P =   x | x | (x)|2 = (x)|2 =   x (- x (- J) = - J) = -   x . x .  J = - J = -   . J = - J = constante . J = - J = constante
donde se observa otra similitud. Aquí <E> es la Energía media, H el hamiltoniano, J la densidad
de corriente (comúnmente llamada Corriente de Probabilidad puesto que aquí | (x)|2 es la Densidad
de la misma). (x)|2 es la Densidad
de la misma).
Por otra parte y según entiendo, ambos Observables cuánticos asociados,
Probabilidad y Potencia (esta última como Energía), no son compatibles, no conmutan:
[P, P ] 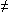 0. Pero esto no ha quitado la
posibilidad de pensarlos al mismo momento, como si los "midiéramos" al
mismo instante. Estas son las conclusiones que se sacan de lo visto precedentemente en
"Analogías experimentales". 0. Pero esto no ha quitado la
posibilidad de pensarlos al mismo momento, como si los "midiéramos" al
mismo instante. Estas son las conclusiones que se sacan de lo visto precedentemente en
"Analogías experimentales".
De esta manera, la cuestión del conocimiento ya cuestionada por Hume y superada su
escéptica por Kant-Laplace, de igual manera se resuelve en este caso (ver el apartado de
mi libro Filosofía Crítica
Trascendental, Cap. 06, § De Hume a Kant-Laplace, y regreso a Aristóteles o mi
artículo en este otro link).
Voy a ampliar un poco aquí el tema y su concepto.
Fruto de una cultura occidental y empirista, la gnoseología de Hume trató a las ideas
cognitivas como fruto de la estructuración cerebral dada únicamente por las percepciones
sensoriales. Esto es decir que los conocimientos no son sino ideas forjadas de la
percepción sensible, de la fenomenología espacio-tiempo. Esto determinó una lógica
agnóstica de la ley de la causalidad, puesto que la misma enlaza a las causas y
sus efectos pero que no puede ser conocimiento. No es fruto del tiempo-espacio. Esto se
conoció como escepticismo de Hume.
Dicha postura ha sido superada por Kant y Laplace, que entiendo se contactaron por vías
escritas, y resolvieron el efecto de una misma manera pero a dos voces diferentes: el
primero a través de los principios de razón (filosofía) y el otro con la física
(matemática). Ambos propusieron un cambio de variable: no usar el tiempo-espacio sino la
frecuencia, y se analizaría entonces esta cuestión desde una manera espectral. Se
conocería esto como convolución laplaciana.
Así las cosas, las cuerdas de la guitarra producen un timbre en tiempo-espacio, aunque
podemos analizar su cuestión como armónicos. Este método no es sino una técnica
abstracta, una ideación cognitiva. Dicho de otra manera, la ley de la causalidad se
entiende pensándola pero no conociéndola puesto que no es fenómeno.
Se dirá sencillamente a Hume que tendría razón y que la fenomenología de la causalidad
en el tiempo-espacio no se la puede conocer, pero eso no nos
impide de que la podamos pensar, como solución del primero.
Obsérvese que se está haciendo lo mismo en la mecánica cuántica. La dualidad de la
experiencia onda-partícula presenta un conocimiento agnóstico y escéptico
fenoménico pero que, cognitivimanete, podemos superarlo al pensarlo
unívocamente, hasta tal vez, como sostengo, con una fuerte correspondencia unificadora.
|
| |
| |
|
Algunas observaciones
No jugando, sino haciendo seria semiótica del lenguaje y su filosofía, a la frase
irónica que entiendo habría dicho Feynman "como se comportan los objetos
cuánticos y esto es cuanto podemos saber de ellos" podríamos
reemplazarla perfectamente por "como se comportan los objetos cuánticos y esto
es cuanto posiblemente
sabemos de ellos".
Presentada la analogía, o en el peor de los casos su similitud, entre la Probabilidad y
la Potencia, será ahora problema de la filosofía el hallar en ello una consideración
satisfactoria. La agnóstica y escéptica respuesta a la comprensión onda-partícula que
hace mérito la mecánica cuántica tendrá entonces nuevos argumentos para entenderla
mejor. Hacer uso de la semiótica, hermenéutica, lingüística, etc. y todas las
herramientas que la filosofía hace del lenguaje comprendo que serán útiles para brindar
un camino diferente, no necesariamente matematico y físico, para dar respuesta a este
interrogante. El mismo concepto de lo trascendental kantiano con su famosa frase
"conocimiento de las condiciones de posibilidad
del fenómeno" muestra a las claras un vasto y amplio camino por recorrer.
De la experiencia cuántica de la doble rendija para confirmar el principio de
indeterminación de Heisenberg, se observa que el análisis geométrico con el impulso p y
su posición x se sustenta en un comportamiento de la gráfica de la distribución
ondulatoria; es decir, que el concepto "onda y
partícula" cobra más sentido que el de "onda o
partícula".
En otros téminos, estamos usando en el mismo tiempo de la experiencia una
interpretación corpuscular para justificar lo ondulatorio. Y por ello, tomando el
concepto que comprendo dio a entender Popper en cuanto a que "la mecánica
cuántica no representa partículas sino más bien nuestro (posible) conocimiento de ellas",
podremos decir que tal vez aquí se halle la respuesta a lo trascendental kantiano
en cuanto a las "condiciones de posibilidades del fenómeno"; esto es, al
contenido de nuestra conciencia en cuanto respecta a las "condiciones"
gnoseológicas.
Por eso, hablar en un mismo momento del "poder de lo probable" (o
"posibilidad de que se pueda") es hablar del "poder de lo que puede
ser" y es esto, en sí mismo, una redundancia o falacia de petición de principio.
Es un juego de términos que no muestran sino una y la misma cosa. ¿Cómo es que entonces
podemos hablar de la Potencia al igual que lo hacemos con la Probabilidad?... pues bien,
será por y en sus "condiciones"que las originan. Allí, en el
contenido gnoseológico motriz que se tiene, tanto físico como metafísico, es que
entiendo radicará la semejanza.
Toda Probabilidad siempre está condicionada, al igual que toda Potencia tendrá una
fuente motriz que la genere. Son similares poderes asociados. Ambas tienen una causa, a
ambas las engendra "algo" como una condición motriz tal cual la premisa del primer
motor inmóvil aristotélico, la correlación cruzada o bien el clínamen
epicúreo. Indagar en esta fuente primaria es hallar una posible respuesta de unificación
al concepto dual onda-partícula.
|
Eugenio
08/09/14 al 28/10/14
Actualizaciones: 20/06/17
Contacto, Mar del Plata, Argentina |
|
|