| |
|
|
INICIO > LA VERDAD
Índice
Introducción
Ejemplo explicativo
Análisis más detallado
La creencia
La persuación
El paradigma desde el enfoque
matemático
La matriz de
correlación que infiere probabilidades
La ponderación de las
argumentaciones
La demostración de algo
Aplicación del Teorema de Bayes
Epistemología práctica
aplicable
El Área de convincencia
Conclusión
Apéndices
Bibliografía
Introducción
Escribir sobre la verdad no es tarea sencilla, puesto que cada uno de nosotros
apetece tener la suya.
Sólo describiré un método que ordenará los pensamientos en este sentido.
Tampoco es una idea mía, sino que se debe a Thomas Samuel Kuhn y que floreció en el
mundo de la filosofía epistemológica en la década del sesenta. Me refiero a su concepto
de paradigma.
Un paradigma es como el constructo de las piezas de un rompecabezas. La imagen
final terminada significará no exactamente una verdad, sino en el mejor de los
casos un acercamiento a una cuasiverdad. Mis colegas epistemólogos comprenderán
mejor lo que quiero expresar.
Las piezas del juego son eslabones que tenemos como certeros, siendo muchas veces
objetivos (universales, compartibles y científicos) y otras como sólo subjetivos (no
científicos, que no podemos compartir y pertenecen a nuestra intimidad solipsada).
Cada uno de nosotros junta estos eslabones y tendrá una construcción dada. Obtendrá una
imagen que se acercará más o menos a la imagen final o cuasiverdad, y
observemos que por ello no necesariamente tendrá las mismas piezas de otro, sino que,
siendo distintas, mostrarán una parte de esta realidad buscada. Seremos nosotros los que
idealizaremos un global conjunto imaginándonos la escena final, tal cual apetece la gestalt.
Así, cada uno de nosotros posee como verdades las partes de un todo y, aquél que posea
más nitidez de conjunto, se acercará con fortunio a vislumbrar mejor la cuasiverdad
esperada. |
| |
| Ejemplo explicativo |
| |
| Vamos a realizar un
ejemplo que aclarará lo que se está exponiendo. |
| |
| Supongamos que tenemos
una imagen que expresará una verdad de contenido: que hay un pequeño perro con un par de
lindos gatitos, refrescándose seguramente en una tina con agua y donde lo acompañan dos
juguetes infantiles: un patito y una pelota al fondo. |
|
| |
| A esta imagen la
fraccionamos tal cual quedarían las piezas armadas de un rompecabezas. A esta figura la
llamamos la verdad de la figura; esto se entenderá, es a donde
queremos llegar. |
|
| |
| Ahora ocurrirá que por
un evento determinado habrá un par de piezas que se han perdido. A esta imagen la
llamaremos cuasiverdad y será, lamentablemente, a la única que
podremos llegar. Sabremos que hay detalles que se habrán perdido, como lo es la imagen
del patito que nunca podremos recomponer. |
|
| |
| Seguidamente
supondremos que hay tres investigadores con respectivos tres paradigmas
de conocimiento: el 1, el 2 y el 3. Cada una de estas personas a logrado juntar las
siguientes piezas y armar por lo tanto los siguientes cuadros: |
| |

|
Paradigma 1 |
|

|
Paradigma 2 |
|

|
Paradigma 3 |
|
| |
Según podemos apreciar
el primero posee 15 piezas, 6 el segundo y 18 el último.
Puede pensarse que la canidad de elementos será el responsable de acercarse mejor
a la cuasiverdad esperada; pero, como realmente vemos, esto no será lo
importante. Para este ejemplo, será el segundo paradigma el que ejemplifique
mejor el contenido puesto que nos da más datos que los otros por contener al perro, a
ambos gatos, a la pelota y también a la tina.
Por eso, se pone en clara evidencia aquí, que la cantidad de hipótesis de una
investigación no necesariamente significará acercarse mejor al resultado fidedigno
esperado.
Y a veces ni siquiera esto, ya que distintos paradigmas pueden mostrar no
solamente parcialidades sino contradicciones entre sus eslabones; y esto porque,
lamentablemente por cierto, se carece de un paradigma más completo que los
contemple.
En suma y con otras palabras, entiendo que siempre se preferirá un teoría que explique
vagamente muchos o todos los puntos de una cuestión o suceso, a otra que explique con
profundidad sólo uno o pocos. |
| |
| |
| Análisis más detallado |
| |
Así como el genio de Descartes en su momento sugirió necesario en una persona que en
algún momento de su vida dude de todo, nosotros deberíamos tener en cuenta que la
conocida frase "percibir (ver) para creer" nos ha enfrascado en un alto y
costoso error del conocimiento de las cosas.
Nuestros sentidos físicos muchas veces nos engañan. Serán conocidos los casos de
alucinaciones en personas como yo he visto padecer, las órdenes post-hipnóticas de
invisibilidad que yo mismo he logrado producir, las equivocaciones mentales que abundan
por doquier como presente en este video, el
engaño y síntesis mental de colores como muestro en este otro ejemplo, etc.
De esta manera y antes de entrar en tema, será necesario definir lo que entendemos por ciencia,
que si bien es una cuestión que muchos creen saber, en realidad hay más gente todavía
que usa su término de una manera vaga y equívoca. Este concepto bien podría tener su
inicio en Heráclito, cientos de años antes de la era cristiana. Conforme la
interpretación en Jaeger, él distinguió el estar dormido (sueño) del estar despierto
(vigilia):
"(...) no tenemos simplemente el símbolo de "los que están
despiertos", sino encima una determinación más precisa del carácter de éstos, a
saber, la de que participan de un mundo común (como prueba su comercio mutuo), mientras
que el mundo de los sueños en que se encuentra el durmiente resulta inaccesible a los
demás." (JAEGER, Werner: “La teología de los primeros filósofos
griegos”, Fondo de Cultura Económica, México, 1952, ed. 1992, pp. 111-128)
O sea que diferenció las experiencias subjetivas de las que no lo son:
las universales, también llamadas objetivas porque pueden ser
observarlas sensorialmente por toda la gente y hacerse con ello de ideas cerebrales que
permitan su análisis y discusión, explicación.
Por consiguiente, llamamos ciencia a todo aquello que podemos explicar y
compartir con el prójimo. Ver Apéndice.
Entrando entonces en tema, quiero decir que estas piezas o eslabones del rompecabezas son,
en sí mismas, también paradigmas. Cada una de ellas apetecerá una cuasiverdad
intrínseca que le caracteriza. Y, a su vez, podrá estar cocausada (condicionada
o correlacionada) con las otras o no. Este último concepto
implica que entre las piezas puede haber causas y efectos que las justifiquen o no como
tales. E inclusive que sirvan para deducir faltantes (en el ejemplo dado, podríamos
deducir el faltante de un objeto si hay alguna o algunas piezas del rompecabezas que de
alguna manera lo expresen)
Será menester aquí tener en cuenta la falacia que se comete al inferir que dos o más
eventos están conectados causalmente porque se dan juntos. Pueden no estarlos. Este error
tiene nombre y se llama cum hoc ergo propter hoc.
A su vez, estos eslabones pueden ser asimismos cuasiverdades subjetivas u
objetivas. Es decir, respectivamente carentes o no de universalidad, de cientificidad.
Por ejemplo, se puede tener una cierta cantidad de hipótesis (eslabones) subjetivas que
no aporten una objetividad deseable, pero bastaría conque uno de ellos sí lo sea y que
se relaciones con los demás como para que todo el conjunto sí apetezca entonces de
cierta objetividad, mínima aunque sea. Tomemos un caso explicativo. Una persona dice
tener vivencias extrañas que no puede explicar, y lamentablemente sabemos que esto
entonces no nos daría aportes objetivos; pero puede ocurrir que conozcamos a esta persona
y sepamos de su cordura y digna fe, cosa por lo cual entonces esto sí alimentaría toda
su experiencia de un tinte de credibilidad aceptable.
Aquí hemos llegado a la necesidad de explicar otro concepto importante: la falsabilidad de
Karl Raimund Popper. Este concepto nos dice que para que una cuestión sea aceptada
como científica debe ser falsable (vocablo acuñado por este autor); es decir,
que tenga argumentos válidos que permitan explicarlo, refutarlo, mostrarlo, etc. Puede
sumar a este concepto lo explicado en este otro link.
Por ejemplo alguien puede decir que mañana en cierto lugar va a llover cucarachas. Bien,
esto sin más, no es científico porque no deja nada con lo cual uno pueda entenderlo,
justificarlo, relacionarlo, etc. Pero, si en cambio dice esto agregando que será así
porque hace un año atrás ocurrió lo mismo en Indonesia pero con escuerzos, entonces
inmediatamente su apreciación pasa a ser algo científicamente aceptable; aunque sea
ridículo.
En suma, lo que quiero decir en todo esto es que las hipótesis que persiguen una cuasiverdad
pueden o no estar relacionadas, ser o no científicas, pero si de alguna manera se
concatenan entre sí pueden dar un cuadro final de verdad que se acerque con más
efectividad al buscado.
Un tema que le continúa y compite, es que se tenga en cuenta de qué manera se
realiza esta concatenación, si es por medios mecanicistas o biológicos (una persona que
los ordena), cosa que determinará otra segunda cuestión de análisis. |
| |
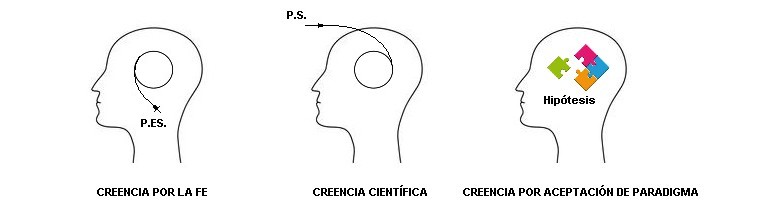
La creencia
De una manera sencilla, si se me permite, quisiera explicar cómo veo yo la manera que
tenemos de creer en algo; esto es, en considerar como cierta una
cuestión. De esta manera y conforme a los desarrollos realizados en mi obra "Filosofía Crítica Trascendental"
se desprende que habría tres maneras posibles:
1º) Por mera fe. Esta funcionalidad no se funda en la
percepción sensible sino en la extrasensible o P.ES. y por tanto subjetivas,
no compartibles con el prójimo. Las ideas que la conforman no
proceden del empirismo sino del racionalismo entendido como sentires
internos (sentimientos). Su hegemonía se daría, tal vez, en el hemisferio cerebral
derecho.
2º) Por conocimiento científico. Se da como fruto de las ideas
empiristas estructuradas y son objeto para compartir con el prójimo a
través de los hechos empíricos (información); le son propios los sentires
externos (sensaciones) o P.S. Su hegemonía se daría, tal vez, en el
hemisferio cerebral izquierdo. Sostienen esta postura autores como Locke, Piaget, etc.
3º) Por el uso del paradigma (correlación).
Consiste en determinar una probabilidad aceptable en función de
eslabones (hipótesis) que nos manifiestan con más explicación que otros la realidad
buscada. Sería, tal vez, funcional con ambos hemisferios cerebrales. Sostendría esta
postura el autor Kuhn.
|
|
La
persuación
No puedo dejar de mencionar esto.
Podríamos considerar que existe una cuarta forma de creencia: por la persuación
de las ideas que confirman una verdad. Si bien no es un método genuino como los tres que
se han presentado, puede entenderse como aplicable al resultado de todos ellos. Veamos en
qué consiste.
Se fundamenta en una "técnica": la de la mensajería y diplomacia.
Así, cuando nos proveen de convincencia a través de datos, mensajes, etc., nosotros
tomamos partido y aceptamos una cuestión como verdadera.
Dicha "técnica" podríamos fácilmente comprenderla con un ejemplo. Supongamos
que hay dos personas y una de ellas desea ir a pasear al campo pero sabe, que si lo pide
directamente a quien la acompañá, habrá una negación. Entonces surgirá el recurso de
la persuación y le comentará que el día favorece y está lindo para pasear.
Seguido, esta otra persona, viendo el acontecer, decide por su cuenta ir al campo juntos.
Así, de esta manera, la primera habrá logrado su objetivo con diplomacia: la
idea ya no le pertenecerá sino que será de la otra persona. Él, con sabiduría, se lo
sugerido hemenéuticamente.
De igual modo, muchas de nuestras conductas como humanos es permitiva e
inteligente, debido a cometidos y apropios afines. No lo olvide.
|
| |
|
|
|
|
|
|
|
El paradigma desde el
enfoque matemático
El tema hegemónico consiste en un sistema que, dadas sus premisas, se deberá hallar su
conclusión. Esto estará exento de la confirmación por la simple percepción sensible,
es decir, que trataremos de llegar a una cuasiverdad a partir de hipótesis no
sensibles.
Supongamos que yo le dijera que la pastilla izquierda del freno de su auto está pintada
de amarillo con lunares verdes. Bien, usted dirá que no es así... Ahora, mi pregunta
entonces es decirle: ¿porqué piensa que estoy en un error? La respuesta será evidente,
puesto que no ha visto nunca ninguna de este tenor y que lo habitual en todas las piezas
del vehículo nunca se distinguen de esa manera. Bueno, entonces, seguidamente, le hago
ver una cosa: si no la ha visto, su seguridad se basa en una correlación de verdades,
esto es, está usando no un conocimiento empírico sino en la utilización del concepto de
paradigma. Esto es, que no lo afirma y cree porque lo ha visto, sino porque correlaciona
verdades. Un juez, por ejemplo, suele usar con frecuencia este método con las hipótesis
de peritos,
testigos, etc. y decide sobre lo que nunca ha visto personalmente. Por ello, se desprende,
que lo que no se ve no siempre es certero, pero puede serlo si sus
correlaciones lo justifican. Así, de manera antagónica, una
verdad como fruto de una percepción sensible podría ser puesta en duda por sus
correlaciones.
Se sabrá que siempre las hipótesis o premisas tendrán un contenido universal probabilístico
de acierto, o bien una subjetividad contingente que otorga el
vocablo posibilidad. Esta diferencia es la que nos proponemos
desarrollar.
Cuando hablamos de información normalmente se piensa que son datos
y eso es un error de cuño. Ellos son considerados como "datos asertivos"; es
decir, que se desprenden de lo apodíctico porque contienen una probabilidad
100% de veracidad. Pero en general debe pensarse que dependen de una factible ambigüedad,
o sea que no tienen 0 [Hatley] sino una incertidumbre que los
acompaña. Y esto es así siempre. Estos "datos asertivos" son sólo un caso
particular y no general.
La matriz de
correlación que infiere probabilidades
Cada premisa tendrá su correspondiente razón probable. Así,
podemos pensar que los sucesos habrán sido fenotípicamente experimentados con
antelación llegando cada uno de ellos a tener las probabilidades
P1, P2,... Pn. La información que los relacionará las
denominaremos respectivamente Ii1, Ii2,... Iin (el subíndice
"i" implica "input") resultando (Ver la ref 1):
Ii1 = log P1 -1 [Hartley]
Ii2 = log P2 -1
...
Ii = log Pi -1 = [Ii1 Ii2... Iin]
> premisa
Dicha premisa de entrada como información Ii a modo de vector, ingresa al
sistema epistemológico G que es una matriz que otorgará la correlación
dándonos la información final de conclusión If (el subíndice "f"
implica "final") que será también un vector. En otros términos, resulta
G = Ii . If-1 > correlación
If = [If1 If2... Ifm] = Ii . G
> conclusión
Si la premisa contiene n elementos (n
premisas) y la conclusión m elementos (m conclusiones), entonces la matriz
epistemológica será de dimensión n X m. Esto quiere decirnos que si lo que buscamos es
una sola respuesta la matriz deberá ser de n X 1 elementos (Ver la ref 2).
Este sistema o canal de de-confirmación se corresponde a lo que se denomina
"Método Inductivista" (M.I.) y que es de mi crítica por ser "ingenuo
o estrecho" como puede ver en este link específico y en este otro
con un análisis estructural del significado del vocablo "ciencia", a diferencia
del generalizado o realimentado del "Método Hipotético Deductivo"
(M.H.D.) que explico, desarrollo y ejemplifico en el Capítulo 3 de Gnoseología de
mi libro "Filosofía Crítica Trascendental".
La ponderación de las argumentaciones
Cuando hablamos de posibilidades, o sea de contingencias, no hay un número que
verifique ninguna ponderación y siempre la cuestión será subjetiva. Sin embargo, toda
nuestra vida de relación, social y eudemonológica, se presenta con decisiones y
pareceres que se fundamentan en esta imprecisión.
Hasta tal punto es la ambigüedad de nuestros aciertos con las cuestiones contingentes
de los pareceres humanos, que el vocablo "equívoco" hace alusión al respecto.
Esto es, que pretende dar por una "fuerte" posibilidad los distintos
pareceres de las personas que opinan al respecto de un tema dado. Dicho término viene de
la dicotomía "equi" que significa "igualdad" y la otra
"voco" que implica "voces"; en otras palabras, igualdad de voces
opinando sobre un asunto. O sea que detona que tiene varias significaciones o sentidos, e
interpretarla como sinónimo de "error" no es lo correcto.
Yo lo que propongo es considerar a esta contingencia, como dijera, con un sentido
"fuerte", positivista. Esto implica que podríamos hablar de una "posibilidad
ponderada".
Quiero expresar con esto que, como lo hacemos recurrentemente y sin darnos cuenta,
inconscientemente quizá, podríamos asignar una cifra a la subjetividad de la posibilidad
como lo hacemos con la objetividad (universalidad) de la probabilidad.
Así la cuestión, llevado la cuestión al análisis epistemológico precedente, si
asignamos subjetivamente una ponderación a una premisa (n premisas), podremos
obtener una conclusión subjetiva y también ponderada, y todo el análisis
anterior se corresponderá.
Con este fin propondré una manera de hacerlo y no quito la factibilidad de que existan
otras más.
Llamaré P a
la posibilidad subjetiva (de una persona o sociedad) como medida
de lo probable P de algo. Esta puede referenciarse como tengamos la asertividad de tener
la certeza o no de un acierto azaroso. Asi 0 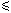 P P 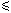 1 y que perfectamente puede ponderase en [%] como
la probabilidad P que es expresada en porcentaje (como se sabrá
a la fracción decimal se la multiplica por 100). Queda entonces: P [%] = 100. P [veces] 1 y que perfectamente puede ponderase en [%] como
la probabilidad P que es expresada en porcentaje (como se sabrá
a la fracción decimal se la multiplica por 100). Queda entonces: P [%] = 100. P [veces]
De manera similar llamaré I a la incertidumbre de una informacion
subjetiva, medida como el porcentaje multiplicando por 100 al Hartley. Asi 0  I [%] = 100. I [Hartley] = 100 /
log P [veces] = 100 / log 0,01 P [%] I [%] = 100. I [Hartley] = 100 /
log P [veces] = 100 / log 0,01 P [%] 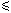 
Consideremos un ejemplo práctico para comprender bien esto. Supongamos que una
persona dice que va a tirar un dado de 6 caras y que el número a salir es el 4. Aquí la probabilidad
es de 1 en 6, o sea una P = 1/6 = 0,166 [veces] = 16,6 [%], lo que determina una información
I = 1 / log P = 0,78 [Hartley]. Pero ocurre que sabemos que esta persona suele mentir y
engañar, cosa por lo cual cada uno de nosotros pensará en
una cierta posibilidad P que es subjetiva y seguramente
lo favorecerá porque el dado estará "cargado". Si yo pienso que es muy
mentiroso, entonces, podría asignarle por ejemplo, una P = 30 [%] de que salga el 4, lo
que me determinaría una incertidumbre I = 1 / log P = 0,5223 [Hartley] = 52,23 [%].
Una ventaja que veo en esta implementación, es que podemos operar conjuntamente e
indistintamente probabilidades (informaciones)
y posibilidads (incertidumbres). O sea
objetividades y subjetividades.
La demostración de algo
Querer confirmar algo fuera de las ciencias matemáticas, siquiera hablar de la "demostración"
de algo en ello, no es sólo utópico y ucrónico, sino peor: es u-epistémico. No existe
eso como tal. Nada se puede demostrar, ni usted mismo puede
hacerlo para decir que está vivo, muerto o lo que fuera.
La convincencia de la certeza apodíctica de una demostración
debe apoyarse siempre en una ambigüedad, es decir en una incertidumbre
y por lo tanto en una posibilidad.
Conforme a mis estudios, investigaciones y presentado el método propuesto, sugiero que
debe plantearse siempre una "línea de demarcación"
en porcentaje de incertidumbre, cosa por la cual superada la
misma nos permitirá ejercer en nosotros toda "Voluntad de
acción""; esto es, ejecutar nuestra conducta en dirección y favor del
argumento.
En otros términos, toda demostración siempre tendrá algo de
ambigüa y jamás le corresponderá una certeza total.
Aplicación del Teorema de Bayes
Quizá, finalmente, de una manera más apropiada y sencilla sea trabajar
directamente con las posibilidades P de un suceso ponderadas como probables P. Esto es, asignar una probabilidad
a un argumento subjetivo. Esto se explico precedentemente. Tomaremos unos simples ejemplos
demostrativos y explicativos donde prevengo al
lector que a ambos los unifico como consideraciones probables (P
= P) para no complicar más las cosas; creo que se comprenderá
cuándo es una apreciación subjetiva de otra que no lo es.
§ - Ejemplo 1. Una persona pensemos que ejemplifica un primer argumento a
contrastar diciendo "Vi un OVNI TR-3B", y otras fuentes periodísticas
de los años 1989-92 nos indican que "En Bélgica se vieron muchos TR-TB".
Si seguido asignamos una probabilidad al evento primero como P(1)=0,1 (10%) y al segundo
como P(2)=0,7 (70%), estaríamos con derecho a suponer que una probabilidad condicionada
entre ambos como que "Se da el segundo dado el primero" P(2/1)=0,9
(90%), entonces por el Teorema de Bayes simplificado se deduce que
P(1/2) = P(1). P(2/1) / P(2) = 0,1. 0,9 / 0,7 = 0,128 (12,8%)
es decir, que esta persona nos ha comentado un suceso que se ha valorizado su
probabilidad de verdad al informarnos del suceso en Bélgica. Pasó de un 10% a un 12,8%.
Y en cuanto a las informaciones respectivas, vemos claramente que se produjo una
información menor de I(1)=1 a la magnitud I(1/2)=0,89, otorgándonos con ello más
asombro su argumento al tener presente lo de Bélgica.
§ - Ejemplo 2. Este es un caso que muestra la potencia de este tipo de
deducciones, aunque pongo en aviso al lector que este ejemplo
requiere revisión, tanto en su planteo como en su concepto teórico. (ref)
Supongamos que el 20% de la gente de una comuna ha visto OVNIs, otro 70% dicen que
no los han visto y el resto 10% no ha conocido la diferencia. El 90 % de los primeros dice
que son de tecnología extraterrestre (seguramente porque los ha visto moverse) y el 1% de
los segundos también (quizá por comentarios al respecto), mientras que los que no
reconocen haberlos visto solamente el 25% dice que lo son. ¿Cuál es la probabilidad de
que uno de ellos elegido al azar piense que es tecnología extraterrestre los haya visto?
Nos valemos para ello del Teorema de Bayes generalizado:
|
P(vieron/ext) = [P(vieron) .
P(ext/vieron)] / [P(vieron).P(ext/vieron) +
P(no vieron).P(ext/no vieron) + P(resto).P(ext/resto)] =
= (0,2. 0,9) / (0,2. 0,9 + 0,7. 0,01 + 0,1. 0,25) = 0,849
|

|
|
donde se observa, que si bien gran cantidad de la gente
no los ha visto y muy pocos de ellos piensa que son de tecnología extraterrestre, casi
todos (84,9%) piensan que sí lo son. Por ese motivo hoy en día, quiérase o no, existe
ya un subliminar social de la existencia extraterrestre generalizado.
Epistemología práctica aplicable
De igual manera que los dos ejemplos anteriores del Teorema de Bayes, he
presentado un par de casos usando el Método Hipotético Deductivo (M.H.D.) como puede ver
en el Capítulo 3 de
Gnoseología de mi libro "Filosofía Crítica Trascendental": uno
para la invención de una vacuna a un ganado y el otro al asertivo de calzados de los
chicos de una escuela.
De esta última prestación deseo rescatar una cosa importancte: el concepto de "umbral".
Aquí la "Información" (o "incertidumbre") del
argumento bajo análisis se ha delimitado en una cota que previamente se ha consensuado
legalmente y llamamos "Información umbral" (Iu) o límite aceptable.
Esto a su vez determinará una "Probabilidad umbral" como Pu =
1/antilog Iu
Este concepto siempre será útil como "línea de demarcación" para aceptar o
no si existe la esperada "demostración de verdad" de
un argumento.
§ - Ejemplo 3. Siguiendo con los ejemplos, aquí amigo lector lo importante no son
tanto los números, no, no se fije en ello; sino en el método propuesto.
Supongamos que la Probabilidad de que un habitante de la ciudad
del caso de Phoenix haya visto la formacion OVNI que llamamos P(A) es del
1%. Y la Probabilidad de que las fotos que se obtuvieron sean ciertas P(B) es del 95 %. De
similar manera, entonces, la Probabilidad de que las fotos seas ciertas tras el avistaje
P(B/A) es la misma del 95%. Se da aquí entonces:
P(A) = 0,01
P(B) = 0,95
P(B/A) = 0,95
Se pregunta entonces la Probabilidad de la gente de la ciudad
P(A/B) que haya visto con certeza al OVNI:
P(A/B) = P(B/A).P(A) / P(B) = 0,95. 0,01 / 0,95 = 0,01
o sea 2 Hartley (sería una información alta, o bien su Probabilidad es baja y por eso se
la cuestiona aún hoy en día)
Para el MHD (Método Hipotético Deductivo) se sabe por las referencias dadas que
|
Go 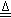 1 [veces] 1 [veces]
 canal inductivista (MI) o de de-confirmación
canal inductivista (MI) o de de-confirmación
Gr 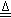 Go / (1 + Go / (1 + 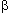 .Go) .Go)  canal deductivista (MHD) canal deductivista (MHD)
Se partirá de una Ii 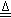 1 [Hartley] por convención referente (podría ser
otra magnitud), o sea de Probabilidad baja del 10 % (algo poco creíble) 1 [Hartley] por convención referente (podría ser
otra magnitud), o sea de Probabilidad baja del 10 % (algo poco creíble) |
|
Donde 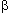 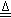 Ir / Ifr
y debe ser armado al revés por estar en un camino de refutación. Esto es decir que la Probabilidad de que sea una foto fake en este caso es baja: Pr(B) =
1- P(B) = 0,05. O bien Ir = log 1/Pr(B) = 1,301 [Hartley] Ir / Ifr
y debe ser armado al revés por estar en un camino de refutación. Esto es decir que la Probabilidad de que sea una foto fake en este caso es baja: Pr(B) =
1- P(B) = 0,05. O bien Ir = log 1/Pr(B) = 1,301 [Hartley]
Así, resulta finalmente
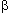 = Ir / Ifr = 1,301 / 1 = 1,301 [veces]
= Ir / Ifr = 1,301 / 1 = 1,301 [veces]
Gr = Go / (1 + 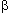 .Go) = 1 / (1 + 1,301. 1) = 0,436 [veces] .Go) = 1 / (1 + 1,301. 1) = 0,436 [veces]
o sea Ifr = 0,436 [Hartley]  Pfr = 0,366 [veces] = 36,6 [%] Pfr = 0,366 [veces] = 36,6 [%]
En otras palabras, la certeza de que un habitante de Phoenix estaría demostrada por las
fotos es de un 36,6 %. Si se aceptara un umbral menor estaría corroborada
(Popper), y si es mayor estaría refutada.
El Área de convincencia
Este último concepto estudiado nos habilita a pensar de que existirá un "Área
de convincencia" donde se acepte el argumento y por tanto se disponga
de suficiente ánimo para ejercer la "Voluntad de acción". La misma se
hallará delimitada por "líneas de demarcación" por Probabilidades (o
bien Informaciones, Incertidumbres) del caso.
Si consideramos por ejemplo una Probabilidad del 80% para que se de tal situación
podríamos pensar que allí se demarca un límite aceptable, que nos produzca seguridad. Y
esto es lo mismo que considerar que posee una Información de prácticamente 0,05
[Hartley], o bien si se me permite que sería lo mismo que decir una Incertidumbre del 5%.
|
Esto entonces delimitará nuestra
segura Área de trabajo ó convincencia mencionada como vemos en la gráfica. Dentro de
ella debemos movernos para obtener realidades y hechos empíricos aceptablemente
esperados.
Sorprenderá al lector de que se ha definido un "Área" y no una
"Línea" operativa, puesto que esto expresa la gráfica que se ha
obtenido de la ecuación I = 1 / log P donde se posee una sola variable que es la abscisa
representando a la Probabilidad.
Bien, lo que ocurre es que al igual que el "mesotés aristotélico"
(equilibrio del término medio) se esperará seguramente otras dimensionalidades, es decir
futuras apreciaciones donde se obtengan más variables de abscisas que determinen a este
caso presentado sólo como una gráfica parcial. Existirán seguramente otros factores
axiológicos (los relacionados con la ética y los valores) que demarquen una
multidimensionalidad del concepto que he querido explicar.
|
|
|
Por lo tanto, para ser más clásicos y seguir una línea de estudio sencilla, ortodoxa,
centraremos nuestra atención en el punto que hemos llamado "Q" como "límite
de demarcación de la convincencia". El mismo se irá corriendo por la curva
conforme a consideraciones axiológicas y/o sociales.
Por ejemplo, un mismo caso ufológico no devendrá la misma ubicación de Q(P,I)
para una persona convencida de la ufología que en otra que no lo esté. La primera
determinará una línea de demarcación con menor Probabilidad que la segunda; o en otras
palabras, será más convincente o convencible.
En esta curva hay un par de puntos Q que quiero destacar:
- El Q(0,1; 1)  Punto escéptico típico
de baja Probabilidad 10% que llamaré Qesc Punto escéptico típico
de baja Probabilidad 10% que llamaré Qesc
- El Q(0,8; 0,0969) 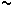 Q(0,8; 0,1) Q(0,8; 0,1)  Punto convincente típico
de alta Probabilidad 80 % que llamaré Qcon Punto convincente típico
de alta Probabilidad 80 % que llamaré Qcon
Siempre es útil, explicativo y aclaratorio tomar ejemplos que muestren los contenidos que
uno expresa. Por este motivo indicaré algunos más de ellos que detallo en los Apéndices. |
|
|
|
|
|
Conclusión
Como conclusión y por ello, yo no hablo de verdad
sino de un acercamiento a una cuasiverdad, dada entonces por una
serie de eslabones (hipótesis) que nos manifiestan con más claridad que otros la
realidad buscada.
Eugenio
14/08/13 - Actualizaciones: 28/07/15, 09/01/16, 07/11/20, 27/03/23, 02/04/23
Contacto, Mar del Plata,
Argentina
Apéndices
Crítica al concepto de
"ciencia" ortodoxo
Lamentablemente no puedo estar de acuerdo con la definición clásica y ortodoxa de la
palabra "ciencia". Sabemos que ella deviene del latín scientia como
"conocimiento" y que sería el conjunto ordenado de conocimientos
estructurados sistemáticamente. (ref)
Pero aquí el problema: hablamos de "conocimiento".
Desde el escepticismo de Hume
sabemos que dicha virtud, el conocimiento, sólo puede darse de las cuestiones
que nos llegan a través de la percepción sensible (PS); y esto niega toda posibilidad de
tener como ciertas las extrasensibles (PES) y/o trascendentes metafísicas.
Por este motivo yo no hablo necesariamente del sentido de las cosas sino de la coherencia
que tienen entre sí y sus correlaciones. (Ver Filosofía Crítica Trascendental, Cap. 13 Filosofía, § El
sentido y la coherencia)
Ejemplos varios sobre cálculos
con el MHD
Les recuerdo y aconsejo que cada vez que pensemos en Información (unidades en
[Hartley] es más visible y práctico hacerlo por su sinónimo epistemológico que es la Incertidumbre
que consideraremos en [%].
§ - Ejemplo de mi experiencia con la
piñata. Me refiero a la experiencia personal que he tenido de la ausencia de una
piñata en un cumpleaños y que he explicado en este link.
Partimos del planteo de la argumentación a contrastar y luego de la constrastadora:
|
- A contrastar: "La piñata ha
desaparecido en el momento del flash fotográfico"  Ii Ii 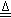 1 (Pi 1 (Pi 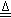 0,1, o
sea 10% de verdad) 0,1, o
sea 10% de verdad)
- Contrastadora: "Se posee la fotografía donde los chicos igual gesticulan su
inminente explosión"  Prealim Prealim 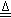 0,999999, o sea 99,9999% de verdad (Irealim
0,999999, o sea 99,9999% de verdad (Irealim 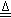 0,000 000
434, o sea 0,000 0434% de Incertidumbre de que sea falso) 0,000 000
434, o sea 0,000 0434% de Incertidumbre de que sea falso) |
|
y procedemos con los cálculos
En otros términos, si nuestro punto Qcon (rojo en la
figura) se halla por debajo del 71,9 % de Probabilidad, entonces el fenómeno será
aceptado como verdadero. Pero como ha dado 71,9% > Qcon sé que mucha gente no lo
aceptará como veraz, pero sí para mi persona que tomó la foto y por tanto el Qcon es
menor.
§ - Ejemplo con n contrastaciones. Supongamos
que se tienen 2 contrastaciones de un suceso (n = 2), donde el argumento inicial es poco
creíble Pi=10% y cada contrastación sí lo son con una Probabilidad de verdad del 90%
cada una. Veamos cómo obtener la Probabilidad final:
obteniéndose finalmente una convincencia del 63,1%, y
donde se puede ver que para que se produzca una alta convincencia, digamos del 80% como un
Qcon, los contrastes deberán ser muchos más: de 10 en este caso:
Para Pfr = 0,8  Ifr = 0,0969 Ifr = 0,0969
Gr = 1/(1+n.1) = 0,0969
n = (1/Gr)-1 = 9,31  10 contrastaciones por lo menos 10 contrastaciones por lo menos
§ - Ejemplo de
verificación del Teorema de Bayes con el MHD
El teorema de Bayes es una herramienta matemática que se utiliza para actualizar
la probabilidad de una hipótesis, mientras que el método hipotético-deductivo es un
enfoque utilizado para probar la validez de una hipótesis a través de la observación y
la experimentación. Ambas herramientas son importantes en la investigación científica y
se utilizan de manera complementaria para mejorar la comprensión y la verificación de
las hipótesis científicas. El método hipotético deductivo puede
ayudarnos a formular una hipótesis inicial y a deducir predicciones a partir de ella.
Podemos usar [también] el teorema de Bayes y otras herramientas estadísticas para
realizar pruebas empíricas y evaluar nuestra hipótesis. Si nuestra hipótesis se
confirma, podemos tener mayor confianza en nuestra comprensión del problema.
(chat.openai.com - 30/04/23)
Seguido tomaré un ejemplo que requiere revisión, prevengo
al lector que puede estar en un error.
Si la probabilidad de que a un alumno seleccionado al azar le guste el helado es del 60 %,
mientras que la probabilidad de que a un alumno le guste la torta es del 36 %. Además, se
sabe que la probabilidad de que a un alumno le guste la torta dado que le gusta el helado
es del 40 %. Calcular la probabilidad de que a un alumno le guste el helado, dado que le
gusta la torta.
Tenemos los siguientes datos:
h  que a un alumno le guste el helado
que a un alumno le guste el helado
t  que a un alumno le guste la torta
que a un alumno le guste la torta
P(h) = 0,6  I(h) = 0,2218 I(h) = 0,2218
P(t) = 0,36  I(t) = 0,4437 I(t) = 0,4437
P(t|h) = 0,4
Entonces aplicamos el Teorema de Bayes:
P(h/t) = P(h). P(t/h) / P(t) = 0,6. 0,4 / 0,36 = 0,6667
Y ahora con el MHD:
1 - P(t/h) = 0,6  Ir = 0,2218 Ir = 0,2218
Gr = Go / (1 + 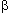 .Go) = 1 / (1 + 0,2218. 1) = 0,8184 .Go) = 1 / (1 + 0,2218. 1) = 0,8184
If(h/t) = Gr. I(h) = 0,8184. 0,2218 = 0,1815  P(h/t) = 0,6583 P(h/t) = 0,6583
Donde observamos que nos daría prácticamente el mismo porcentaje.
Bibliografía
KUHN, Thomas S.: La estructura de las revoluciones científicas (1962), trad. por
Agustín Contin, 11a ed., México, F.C.E., 1995.
TAIT, Eugenio Máximo: Filosofía
Crítica Trascendental, Año 2000 |
|
|
|
|